Tangent Circles

Assignment 7

By Erin Cain

In this problem we are asked the following:

Explore the following: given two circles and a point that lies on one of the circle, construct a circle tangent to the two circles with one point of tangency being the designated point.

Let’s start by constructing a circle with a center A, and then constructing another circle inside the first one with a center B.

Next we will place points on both circles and we will label them C and D. Point D will be the designated point of tangency of the circle we are about to construct and circle B.

Next we need to construct a line through points A and D. The center of the tangent circle will actually lie on this line. We will then construct the radius of circle B by constructing the line segment BC. We can now use this as the radius of a circle with a center at point D.

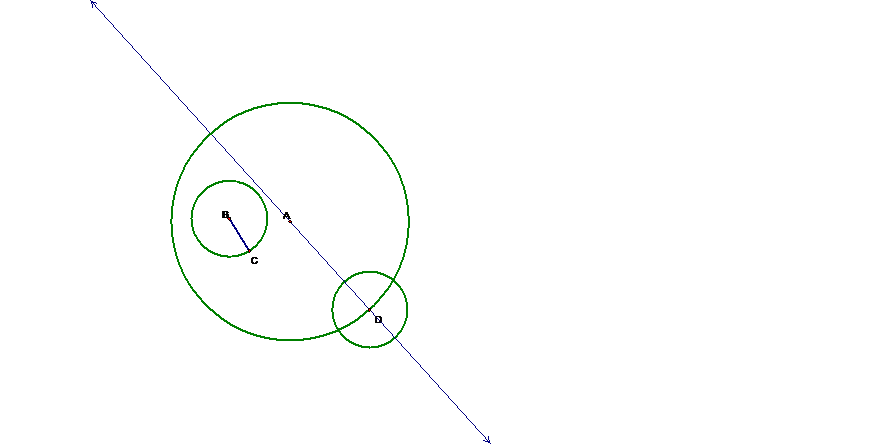
Next we need to construct a line segment that has an endpoint at B and the other endpoint at the point of intersection between line AD and circle D.

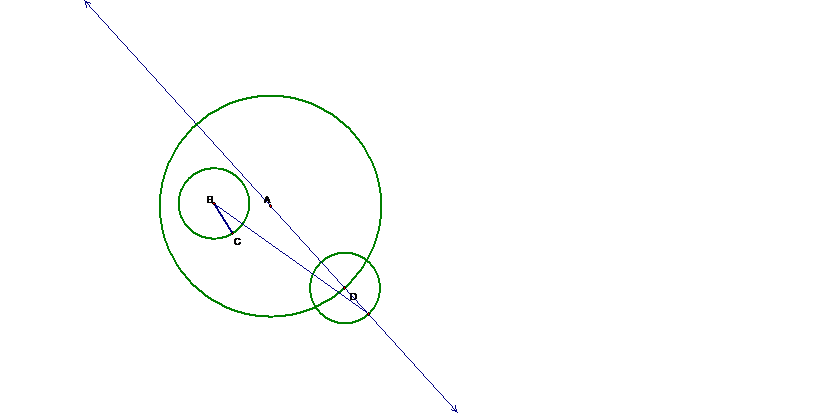
Here we can construct the perpendicular bisector of the line segment with endpoint B and the intersection of line AD and circle D. The radius of our tangent circle will be the length of the segment DE. Note that E is shown in the picture below. This tangent circle will be centered at E, and we can now use the above information to construct the tangent circle. We know that the center of the circle will lie on the line AD, therefore we can mark the intersection of the perpendicular bisector just created and this line, point E, and this is the center of the tangent circle. 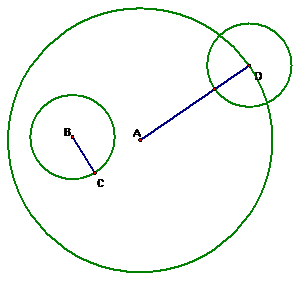Because the tangent circle being created must be tangent to both circle A and circle B, we can use D as the point we want our tangent circle to go through. Now by constructing a circle by center-point, we will have a circle that is tangent to both circle A and circle B.

Click HERE for a script tool that you can use to create your own tangent circles.

Now I want to take a look at the locus of the center of the tangent circle, point E, as point D moves around circle A. Click HERE to see an animation of this in GSP. By watching this animation, we can see that the locus of E will be an Ellipse. The ellipse will change in size when the point B is moved to different locations within circle A as well as when B is moved outside of circle A. The size and shape of the ellipse will also change when circle B changes in size.

Let’s look at a different tangent circle now. I now want to look at one that is tangent to the outside of circle B and also tangent to circle A. To go about constructing this, similar to what we did before, we need to construct point D on circle A and draw in the radius. Then by using a circle, we need to mark off the radius of circle B on the segment AD.

Now I will label the new intersection point E and connect points E and B. I can now create an isosceles triangle by constructing the perpendicular bisector of this line segment and to find point F on the radius of circle A.

Now I am able to construct the tangent circle (red) by using FD as the radius.

Click HERE to use the script tool so that you can create this type of tangent circle yourself. Let’s now explore the locus of the center of the tangent circle F. This needs to be done in cases though.

The first case is when circle B is inside of circle A. In this situation, the locus of center F will be another ellipse with foci of F and B. You can watch this animation HERE. The next case we need to look at is when circles A and B intersect. In this case, the locus of F will be a hyperbola. This animation is available HERE. Last but not least, the third and final case is when circle B is completely outside of circle A. Once again we will have a hyperbola. You can watch the animation of this HERE.

RETURN