Ceva’s Theorem
Final Assignment
Part B
By Erin Cain
In this problem we are asked
to explore Ceva’s Theorem.
Consider any triangle ABC. Select any point P inside the triangle and
draw lines AP, BP, and CP extended to their opposite sides in points D, E, and
F respectively.
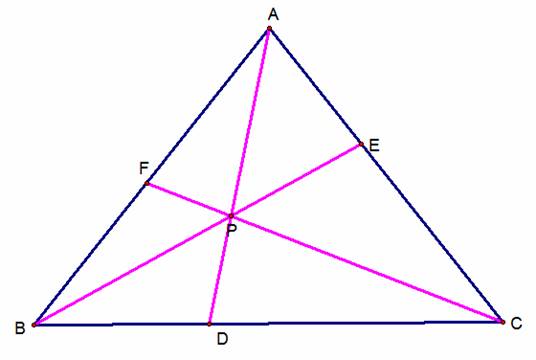
1)
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various
triangles and various locations of P.
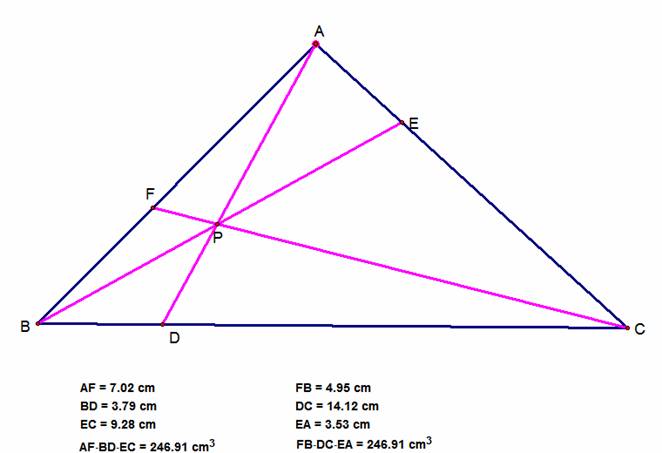
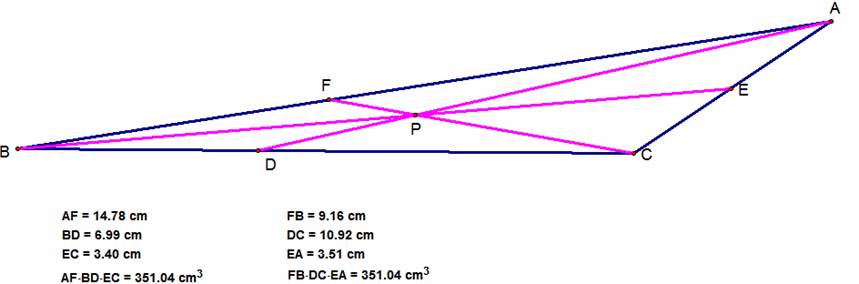
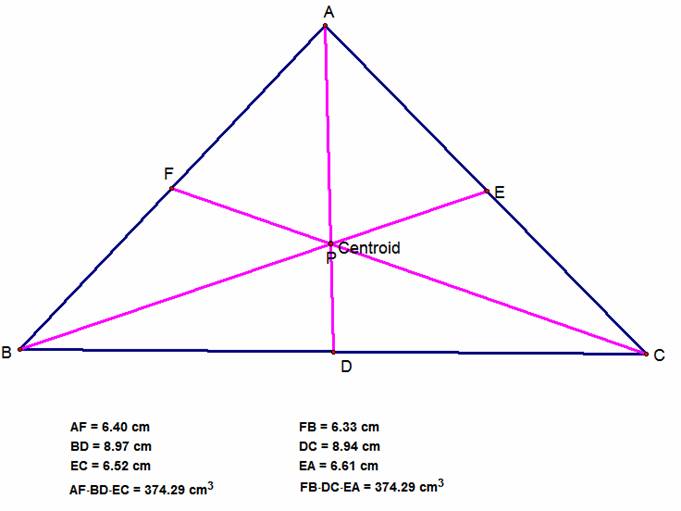
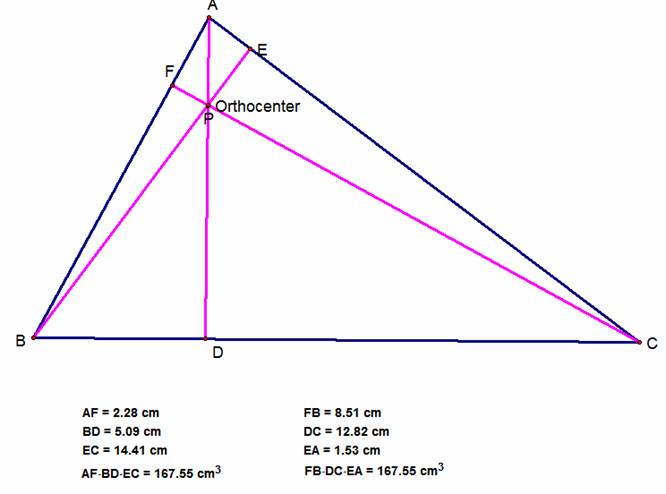
As you can see from the above
pictures, no matter what kind of triangle you are looking at, and not matter
where P is located, the products (AF)(BD)(EC) and (FB)(DC)(EA) are always equal
(to manipulate this triangle on your own, click HERE). Therefore, the ratio of the two products will
always be one. This is Ceva’s Theorem.
In order to prove that this
is true, we must show that if AD, BE, and CF are concurrent if and only if the
product of the ratios equals one, i.e.
(AF)/(FB) * (BD)/(DC) *
(CE)/(CA) = (AF * BD * CE) / (FB * DC * CA) = 1.
To begin our proof, we will
use our point of concurrency, P, to form three triangles, PAC, PCB, and PBA.
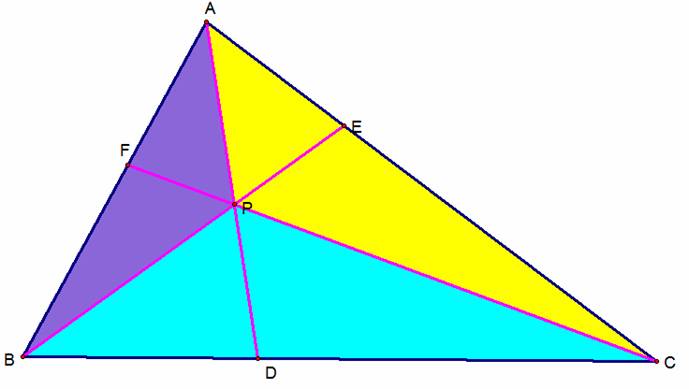
Next we can construct line
segments from P that are perpendicular to all three sides of our original
triangle, ABC (the black, dashed lines in the picture below). These line segments become the altitudes for
these three triangles.
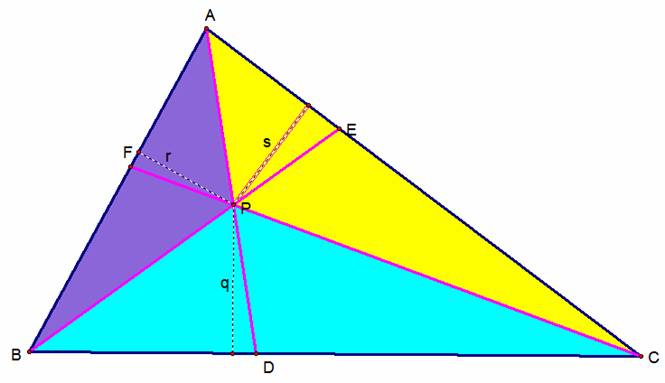
When looking at the above
picture, there are actually six different triangles inside of our original
one. Therefore, our altitudes, q, r, and
s, are the altitudes for two different triangles.
q is the altitude for triangles BPD and DPC
r is the altitude for triangles BPF and FPA
s is the altitude for triangles APE and
Now that we know the altitude
for each of these triangles, we can use this to compare the areas of the
triangles (note that the altitude of a triangle equals the height of a
triangle. Let’s look at the ratio of the
area of triangle
Area(
Area(EPA) = (1/2)EAs
Area(
Area(
Due to the fact that they
share the same altitude/height, both the ˝ and the altitude in both areas will
cancel each other out (i.e. when you divide them you will get a quotient of
1). This holds true for the rest or the
triangles. Therefore, we have the
following:
Area(BPD) / Area(DPC) = BD / DC
Area(FPA) / Area(BPF) = FA / BF
Therefore we have the
following:

QED.
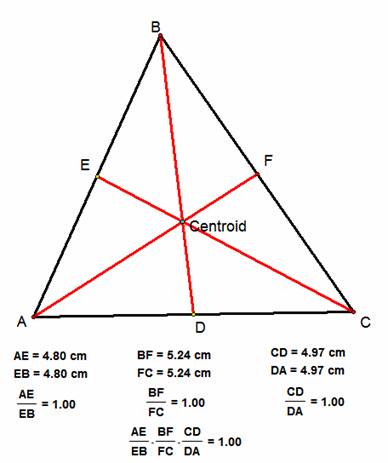
How can this theorem be used in proving concurrency of
the medians if P is the centroid?
The
fact that the medians of a triangle has a point of concurrency is one of the
easiest ideas to prove with the use of Ceva’s Theorem. A median is a line that connects the midpoint
of one sides of a triangle to its opposite vertex. Therefore, a median divides the side of a
triangle into a ratio of 1 to 1.
Therefore, when you a triangle has all three medians drawn and you find
the product of the ratios of the sides, you will be multiplying ratios of 1 to
1, hence the product of the ratios equals one.
By Ceva’s Theorem, they must have a point of concurrency, which is the
centroid of the triangle.
How can this theorem be used in proving concurrency of
the lines of the altitudes if P is the orthocenter?
This
can be done similarly to the proof above of Ceva’s Theorem. When you draw in the altitudes of a triangle,
you essentially divide the original triangle into six smaller triangles. Unlike the proof above, the altitudes are
already drawn for each of the smaller triangles. Therefore, you can set up the ratios and find
that the product of the areas of each of the smaller triangles equals the
products of the ratios of the sides of the triangle, which in turn equals
1. Therefore there the altitudes of a
triangle have a point of concurrency which is the orthocenter.

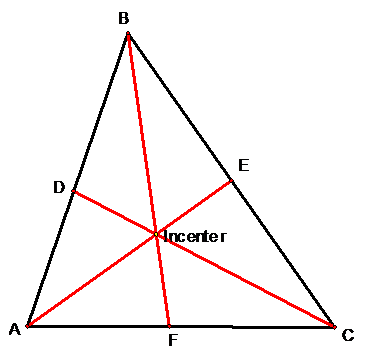
How can this theorem be used in proving the
concurrency of the angle bisectors if P is the incenter?
Similar
to above, you can prove the concurrency of the angle bisectors of a triangle
simply by proving Ceva’s Theorem when P is at the incenter. Once again, you end up with six smaller triangles
when you construct the angle bisectors.
If you take the point of intersection and construct perpendiculars to
each side of the original triangle, you will have created all of the altitudes
for the six triangles (the two triangles on the same base share the same altitude). Form here you can follow the same steps for
proving the concurrency of the altitudes of a triangle or the steps for proving
Ceva’s Theorem.
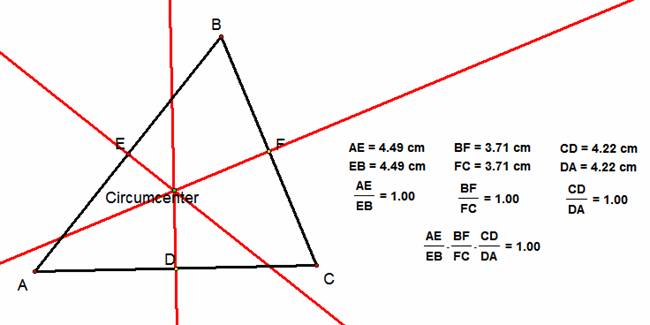
How can this theorem be used in proving the
concurrency of the perpendicular bisectors if P is the circumcenter?
Similar
to proving the concurrency of the medians of a triangle, perpendicular
bisectors divide the sides of the triangle into a 1 to 1 ratio. Therefore, the product of the ratios of the
sides will equal 1, and for this reason, the perpendicular bisectors have a
point of concurrency at the circumcenter of the triangle.