HYPERBOLA

By

SHADRECK S CHITSONGA

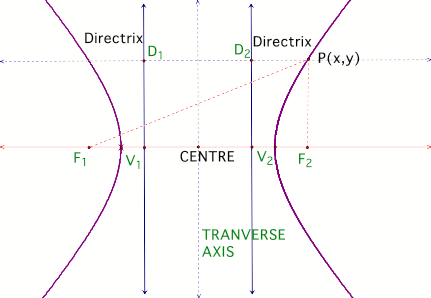
Let us firstly look at the main features of a curve known as the hyperbola. The diagram below shows the main features of the hyperbola.

A hyperbola is a set of points (x,y) in the plane whose distances from two fixed points have a constant difference. The two fixed points are called the Foci. Unlike the parabola that has one continuous curve, the hyperbola is made up of two branches and two foci as.

In the diagram below V1 and V2 are the vertices.

In a hyperbola the ratio PF1/PD1 is the same as the ratio PF2/PD2.

This ratio is known as the eccentricity of the hyperbola.

Though the diagram below is not drawn to scale it is clearly that this ratio is certainly greater than 1.

Without going into rigorous mathematics, just look at the (rectangle) D1 P F2 V1 , PF1 is greater than the diagonal of this rectangle, therefore greater than PD1( Applying Pythagorean Theorem). The hyperbola shown in figure 1 has its transverse axis parallel to the y-axis.

Figure 1

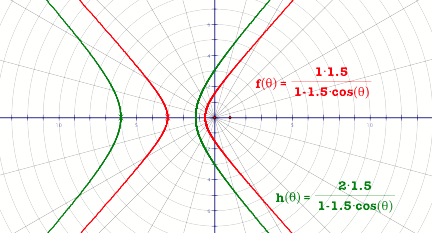
Continuing with our discussion on the graphs of functions of the form r=

We will now consider the case when e is greater than 1, and look at different values of k.

In the case of the parabola the value of e is exactly one.

Figure 2

In this case the eccentricity is greater than one and the curve we get is a hyperbola.

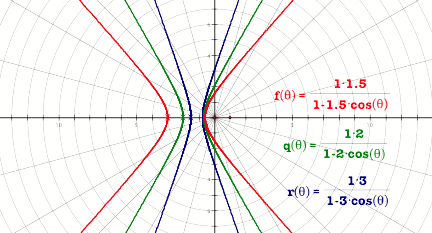
What happens when the values of e and f are changed?

Changing the value of k seems to change the location of centre of the hyperbola. As the value of k increases the branches of the hyperbola are pulled further apart. The value of k determines where one branch of the hyperbola crosses the y-axis.

For example if k = 2, the curve crosses the y-axis at (0,2) and (0,-2).

Increasing the value of e brings the branches of the hyperbola close together.

Figure 3

CLICK to open GSP to see what happens when the denominator has a positive sign instead of the negative sign. What is your conclusion? What features if any of the graph are affected by this?

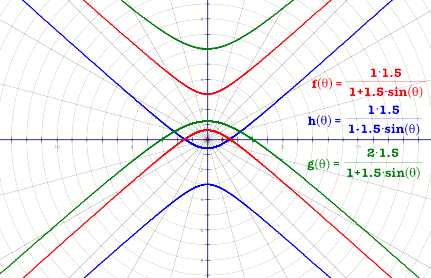
We will now investigate the effect of having a sine function in the denominator rather than cosine.

Look at figure 4.

Figure 4

There are a number of observations we can make here.

1. All the three curves shown above have their transverse

axis parallel to the x-axis. Compare this to when there

is cosine in the denominator.

2. The curves that have a +sin q in the denominator have

there tranverse crossing the positive y-axis and with

-sin q, the transverse axis crosses the negative y-axis.

3. The product of the denominator (ke) determines the

point where one of the branches of the curve crosses

the x-axis.

4. Keeping everything constant, the higher the value of k,

the further the curve moves up along the y-axis.

END