ASSIGNMENT 3

BY

SHADRECK S CHITSONGA

PARABOLA AS THE LOCUS OF VERTICES OF OTHER PARABOLAS

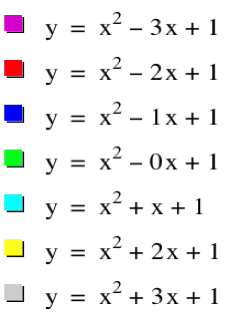The graphs shown in figure 1 are graphs of the function

The values of b are set at -3,-2,-1, 0, 1, 2 ,3. Figure 1

There are a number of things that we know from our study of quadratic functions. Though that is not the main focus of this write up, we will mention the following things.

1. All the graphs are concave up because the coefficient of is positive.

2. All the graphs pass through the same point, that is (0,1), because all the functions

plotted have the same value of c, c =1.

3. All the graphs have different vertices, they have different values of b.

We will expand on number 3 further. Let us go back to the basics of quadratic functions. Any quadratic function is of the form .We know that the line of symmetry is at x=-b/2a, From our examples above the vertex is at .

Look at the vertices of the functions whose graphs are plotted in figure 1:

FUNCTION VERTEX

(1 , 0)

(0, 1)

(-1,0)

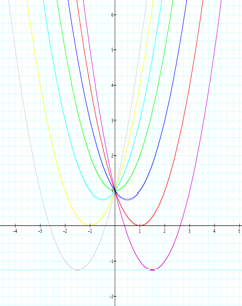
Now that we have the vertices we can plot the points to determine the relationship between x and y for the vertices. Figure 2 shows the vertices as plotted in GSP

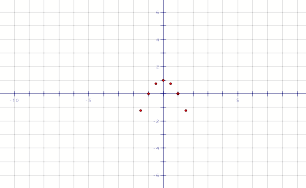
Figure 2

Clearly we can see from the plot that this curve is that of a parabola. It is not difficult for us to determine the equation for the function that generates this parabola. This curve crosses the x-axis at -1 and +1. This implies that the equation is (x-1) (x+1)=

But the curve is concave down, so the equation is y=-()

Figure 3 shows that the locus of the vertices of the set of parabolas graphed from is the parabola

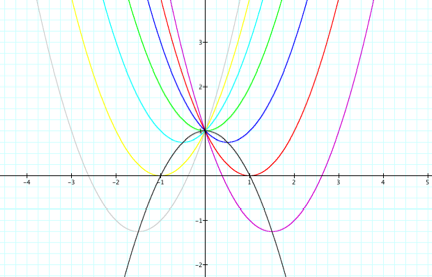
Figure 3

Can we write a general result here? Let us look at the original function . Where c =1.

Observe the following:

1. The coefficient of is -1 while in the original it is 1.

2. The original expression has b in it. The new expression has the value of b as 0.

3. The original equation has c =1 and the new equation has c=1.

It looks like we can conclude that for the function the resulting parabola will be

Before we may a sweeping statement. Let us consider the graphs below to see if our conclusion is indeed valid.

Let us consider the function , where the values of b are as before.

Here if our conclusion from the previous example is true then we expect the locus of the vertices to be the parabola . We will plot all the functions together and see whether this parabola will indeed pass through the vertices. Refer to figure 4.

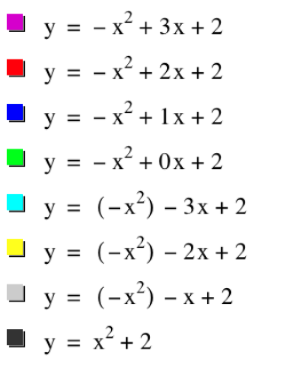
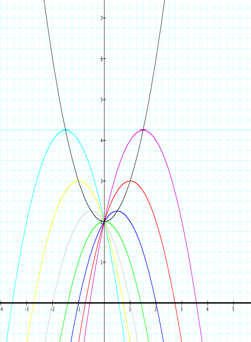
Figure 4

In conclusion we can say that as long as a and c remain constant, the vertices of the parabolas generated by , will always be .

END