ASSIGNMENT 1

BY

SHADRECK CHITSONGA

EXPLORING GRAPHS MADE BY THE PAIRS OF LINEAR FUNCTIONS

The general linear function is of the form f (x) = ax +b, where a and b are constants.

If a = 0 then f (x) = b is just a line parallel to the x-axis that passes the y-axis at the

point (0,b). If b=0 then f (x) is a line that passes through the origin. This is non-vertical line.

CASE 1: The sum of two linear functions

Below we have two linear functions:

f(x)=3x=4 and g(x)=2x+5.

We will consider the function that is made up but summing up the two functions,

 i.e. h(x)= f(x) +g(x) therefore h(x) = (3x+4) +(2x+5)

=5x+9

We see that h (x) is of the form f (x)= ax + b , this means that h(x) is another linear function.

This is confirmed by the graph shown in figure 1. The graph is for

y =5x+9

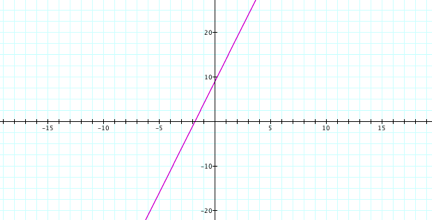
Figure1

Observation:

The resulting linear function will have the following properties:

 1. The slope of the line of the function will be the sum of the

slopes of the lines of the individual functions..

2. The y-intercept will be the sum of the individual

y-intercepts. In general we can say that,

if h(x) = f (x) + g (x)

= (ax + b) + (cx + d)

=(a + c)x+(b + a)

then the slope of the line will be (a + c) and the y-intercept will be

(b + c)

Question:

Will the x-intercept for the line of the function h(x) be the sum of the x-intercept of the lines for the functions f(x) and g(x) ? Discuss.

CASE 2: The product of two linear functions

 Define h(x)= f(x) g(x) where f(x) and g(x) are linear functions.

 Using the same functions as above we have

 h(x)=(3x+4)(2x+5)

       =6x(^2)+23x+20

h(x) is of the form p(x) = ax (^2)+ bx +c, which is the general form of a quadratic function, this implies that h(x) is a quadratic function. The graph in figure 2 shows that we get a U- curve, which is a parabola.

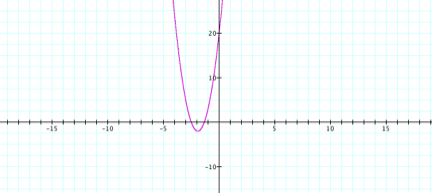
Figure 2

CONCLUSIONS

1. The product of two linear functions is a quadratic function.      

    In general if f(x) = ax + b and g(x) = cx + d

=(ac)x(^2)+(ad+bc)x+bd)

=a'x(^2)+b'x+c'( a quadratic function)

Where a' is the product of the slopes of the lines of the two original function   b' is the sum of the product of the slope of the first line and the y-intercept of the second line and the product of the intercept of the first line and the slope of the second line. c' is the product of the y- intercepts of the two lines.

Question

If h(x)= 6x(^2)+36x+30 , where h(x)= f(x)g(x),

If f(x) =2x+3,find g(x).Discuss a number of methods you can use to find g(x).

CASE 3: The quotient of two linear functions

Define h(x)= (f(x)/g(x)

Using the same functions that we used in cases 1 and 2, we now draw the graph of h(x).

The graph is shown in figure 3.

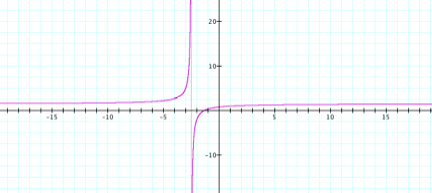
Figure 3

By definition h(x) is a rational function, this implies that the  quotient of two linear functions is a rational function. There are a number of things worth noting about graphs of rational functions. While exploring the functions on a graphing utility it is important that the students understand the various components of the graph.

The following might be important to mention:

1. The range and the domain of the rational function.

2. The asymptotes, both horizontal and vertical. How are these

values found?

QUESTIONS

a. Is the any connection between the x- intercept and any of

the two linear functions?

b. How does changing the sign on the coefficient of x affect

the graph of the resulting function?

c. In our graph above the asymptote is the line x=-4/3. This is

the vertical asymptote.   Is there a way you can tell from

the two linear functions where this is coming from?

d. Under what circumstances do we get the horizontal

asymptote?