EXAM
BY
SHADRECK
S CHITSONGA
BOUNCING
BARNEY
QUESTION
Barney is in
the triangular room shown here. He walks from a point on BC parallel to AC.
When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he
turns and walks parallel to AB. Prove that Barney will eventually return to his
starting point. How many times will Barney reach a wall before returning to his
starting point? Explore and discuss for various starting points on line BC,
including points exterior to segment BC. Discuss and prove any mathematical
conjectures you find in the situation.
Let us start
by looking at the GSP diagram shown in figure 1. Pay special attention to the
parallel lines and the lengths of the distances.
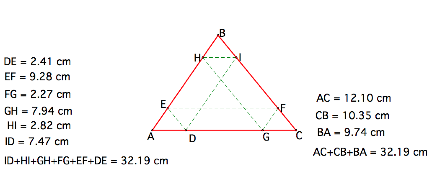
Figure1
In figure 1,
Barney starts at point I on the side BC. He moves on IH parallel to AC to reach
H on AB. Then moves HG parallel BC to G on AC. From there he moves GF parallel
to AB to reach F on BC. From F he moves FE parallel to AC to reach E on AC. He
then moves ED parallel to BC to reach D on AC. Finally he moves DI parallel to
AB to reach I on BC.
Looking at
the diagram and the distances shown, there are a number of conjectures one can
make.
1. The distance that Barney covers from
the starting point
back to the same
point is equal to the perimeter of the
triangle.(Note:
Barney is starting on a given side of the
triangle). CLICK here to see whether the same thing holds when
Barney starts from
another point on a different side of the triangle.
Drag point D along
the side AB.
2. To complete his journey, Barney must
reach each wall of
the triangle twice.
In total Barney travels in six segments to return
to the starting point. For an exception see part
3.
3. If Barney
starts from the point that is the mid-point of a
side of the triangle,
Barney reaches each wall once before
returning to the staring
point. He moves parallel to each
side once. (CLICK HERE for the diagram)
For our
proofs let us start by looking at a specific case.
We will
consider a situation when Barney starts from the point that is the mid-point of
a given triangle.
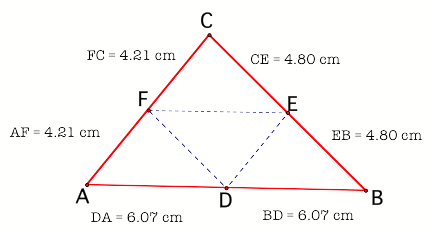
Figure 2
We started
with D as the mid-point of side AB, and constructed DF parallel BC, then FE
parallel to AB and finally ED parallel to AC. Just by looking at the distances
measured we see that F and E are also the midpoints of sides AC and CB
respectively. That should not be a surprise because of the intercept theorem.
Let us forget
the distances and write a formal proof.
Proof
In the ![]() ABC, D is the
mid-point of AB (given)
ABC, D is the
mid-point of AB (given)
DF is
parallel to BC (construction)
Therefore FD
bisects AC (mid-segment theorem)
AF = FC
Now D and F
are the midpoints, it means that
FD = (1/2)
BC, Similarly FE parallel AB, which means that
CE = EB, and FE = (1/2)
Since E is
the mid-point of BC, a line drawn through E parallel to AC must pass through the
mid-point of side AB. In this case we know that the mid-point of AB is D,
therefore this line passes through D.
Also ED =
(1/2) AC.
Conclusions
from the proof:
1. From the
proof we can see that the total
distance Barney
covers is equal
to FD + FE + ED=(1/2)
BC + ( 1 / 2) AB
+(1/2) AC.
=(1/2){BC + AB + AC}
= (1/2){perimeter of ![]() ABC}
ABC}
2. The proof
is showing us that if Barney starts
from the mid-point , he
ends up at the mid-point.
Proof to
show that the distance Barney covers is equal to the perimeter of triangle ABC
if Barney starts from any point on the side other than the midpoint
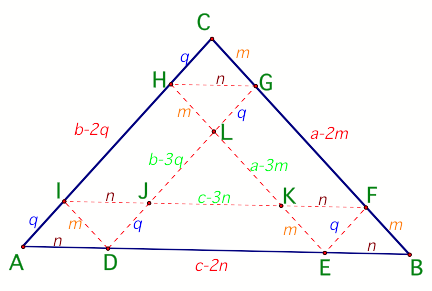
Figure 3
The perimeter
of ![]() ABC is given by AB + BC + CA. This is equivalent
ABC is given by AB + BC + CA. This is equivalent
to a + b +c (
where c = AB , a= BC b= CA )
Because of
the number of parallel lines we have drawn in the diagram, it is easy to see
that we have a number of parallelograms formed. In the diagram, the lower case
letters are standing for the length of each side, for example the length of ID=
m, the length of DE=c-2n.
Now let us
trace the path Barney takes. We will start from D on AB and follow the path
through DI, IF, FE, EH, HG, and GD.
Adding all
the distances we see that:
DI+ IF+
FE+EH+HG+GD = m +n +c-3n +n+q+m+a-3m+m+n+q+b-
3q+q.
=3m +3n +3q-3m-3n-3q+a+b+c
= a + b+ c
=
perimeter of ![]() ABC
ABC
______________________________________________________________________________
Proof to
show that Barney will return to the starting point
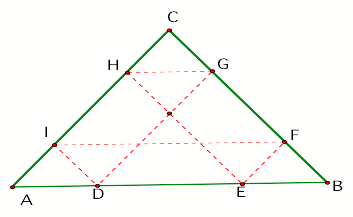
Figure 4
We now want to prove in general that no matter where Barney starts from, he
will end up on the same point. We will still consider D as the starting point.
Our proof will mainly involve the application of the basic proportionality
theorem also known as Thales.
Theorem.
If a line
is drawn parallel to one side of a triangle intersecting the other two sides,
then the other two sides are divided in the same ratio.
Proof
(Barney’s Journey)
Given triangle
ABC with D a point on side AB.
But AD is
parallel to BC (construction)
![]() =
= ![]() (Constant
proportionality)
(Constant
proportionality)
IF is drawn
parallel to AB,
![]() =
= ![]() (Constant
proportionality)
(Constant
proportionality)
FE is drawn
parallel to BC,
![]() =
= ![]() (Constant proportionality)
(Constant proportionality)
HE is drawn
parallel to AC,
![]() =
= ![]() (Constant proportionality)
(Constant proportionality)
HG is drawn
parallel to AB,
![]() =
= ![]() (Constant
proportionality)
(Constant
proportionality)
If one follows
the arguments above carefully it is
easy to that ![]() =
= ![]() =
= ![]() =
=![]() =
= ![]() =
=![]() (i)
(i)
We can also
see that ![]() ,
, ![]() ,
, ![]()
Now let us go
back and consider the point G, the line from G must be drawn Parallel AC.
Using Thales
Theorem, this line must divide sides AB and AC in the same ratio.
Let us say for
the moment that this line intersects AB at point D*.
GD* is
parallel to AC
and ![]() =
= ![]() (constant
proportionality)
(constant
proportionality)
But
in (i) we showed that ![]() =
= ![]()
This
means that AD = AD* and because A is a common point, we can
conclude that
D* and D are the same point.
YES, BARNEY
WILL RETURN TO THE ORIGINAL POINT.
What about if Barney
starts from if Barney starts from a point exterior to segment BC?
Refer to figure 5
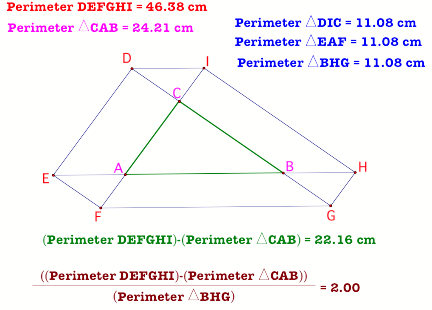
Figure 5
From the GSP diagram
in figure 5, we see that when Barney starts from point D outside segment BC, he
still comes back to the starting point. He completes his journey in six
segments.
Conjecture
If barney
starts from a point outside the segment BC, he covers a distance equal in
length to the perimeter of the original triangle + 2(perimeter of the little
triangles formed at each vertex of ![]() ).
).
The perimeter
of each little triangle is the same as the sum of the three short segments DI,
EF and GH that are parallel to the sides AB, BC and CA respectively.
Proof
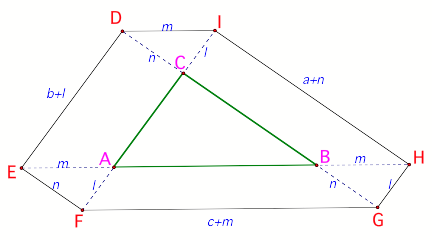
Figure 6
Using
notation in figure 6 it is very
easy to see why the sides are marked that way. For example Segment EF= Segment
BG=n, because EFGH is a parallelogram (by construction).
We can use
similar argument for the other sides.
Note a, b,
and c are the lengths of the sides of triangle ABC.
Therefore the
perimeter of triangle ABC = a+ b + c.
The total
distance Barney travels = a + n + m + b + l + n + c + m + l
=
a + b + c + 2 ( m + n + l )
= perimeter of ![]() ABC + 2(sum
of
ABC + 2(sum
of
the lengths of short segments.
Other
observations
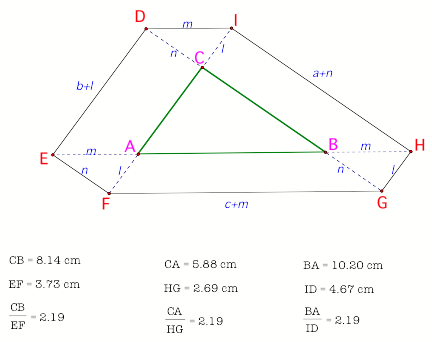
Figure 7
Consider the
short segments DI, GH, and EF and the ratios shown in figure 7.
We see that
all the ratios are equal. Each one is equal to 2.19 in this case. Will this be
always the case, that the ratios will be equal?
Let us write
a short proof.
Consider ![]() AHI and
AHI and ![]() ABC
ABC
![]() (Constant
proportionality) (i)
(Constant
proportionality) (i)
In ![]() BED
and
BED
and ![]() BAC
BAC
![]() (Constant proportionality)
(ii)
(Constant proportionality)
(ii)
In ![]() CFG
and
CFG
and ![]() CAB
CAB
![]() (iii)
(iii)
Putting (i),
(ii), and (iii) we have ![]()
CONCLUSION: All
the ratios are the same.
_____________________________________________________________________________