ASSIGNMENT
4
BY
SHADRECK S CHITSONGA
THE
MEDIANS OF A TRIANGLE
In this write up I will explore
some of the interesting properties of the medians of a triangle. Let us first
of all define a median.
A median of a triangle is a
line segment that joins the vertex of a triangle to the midpoint of the
opposite side.
There are some basic facts
about the medians, which I will just mention and can be explored easily in GSP.
Here are some of them:
a. In any triangle there can
only be three medians.
b. In an equilateral triangle
all the medians are of the same length.
c. In an isosceles triangle,
the two medians drawn from
the vertices of the equal angles are equal in
length.
d. In a scalene all the medians
are of different length.
e. The medians are always
inside the triangle.
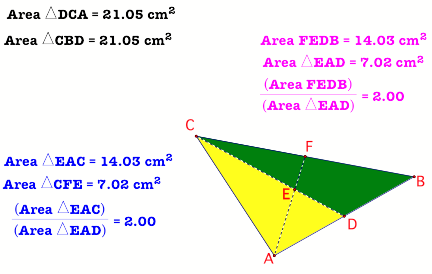
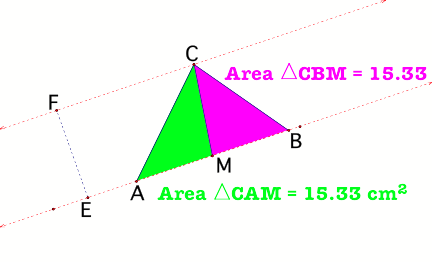
1. MEDIANS AND AREA
One median
Figure
1
From the diagram in figure 1 we
see that the two triangles CMA and BCM are equal in area. We can come up with a
conjecture and say that, the median of a triangle divides the triangle into two
triangles with equal areas.
To show that this is always
true we can write a short proof:
Area of any triangle = half the
base x height.
In the triangles CMA and CBM,
AM and MB are the bases respectively. The two triangles have the same height.
Therefore area of triangle CMA=
½(AM)(FE)
And area of triangle
CBM=1/2(MB) (FE)
From the two areas we see that
FE=FE (the two triangles have the same height).
Also AM=MB (M is the midpoint
of AB, since AM is the median of the triangle. This then means that the two
triangles are equal in area.
Now let us consider two
medians. Look at the diagram below. We want to see if we can say anything else
about the areas.
We have already seen that the
median divides the triangle in two equal areas.
Let us extend that and see what
happens when we put in the second median.
Look at the GSP diagram in
figure 2
Two medians
Figure
2
We have already shown than the
median divides the triangle into two triangles of equal areas (look at the
green triangle and the yellow triangle).
Let us say that CD is the first
median, this divides the triangle as explained above. Now consider the second
median, AF. It intersects with the first one at E. We notice that the second
median divides the green and yellow triangles in the ratio 1:2. We can write a
conjecture here,
If a median one median of a
triangle is drawn, the second median to be drawn will divide the areas of the
two triangles formed by the first median in the ratio 1:2.
We will postpone the proof for
now as we proceed to the case where there are three medians.
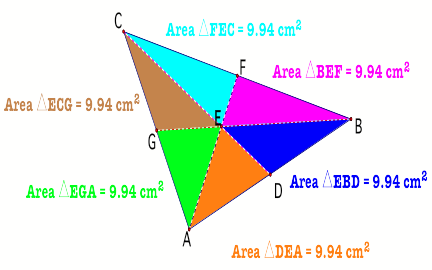
Three medians
Figure
3
From the areas calculated it is
easy to see that after drawing all the three medians the original triangle is
divided into six triangles that are all of the same area. Another thing we have
noticed is that the three medians are meeting at the same point (All they are
concurrent).
Conjecture
Three medians of a triangle
divide the triangle into six triangles that are all equal in area.
PROOF
Let us use the same triangle
ABC we have in figure 3.
Triangles AED and EDB have the same attitude since they share
the same vertex and are sitting on the same base AB.
But we know that D is the
midpoint of AB (CD is the median).
It then follows that the area
of triangle AED is equal to the area of triangle EDB.
Earlier on when we considered
the case of two medians we saw that the second median divided the two triangles
formed by the first median in the ratio 2:1. Using that argument we know that
the area of triangle AED is 1/3 the area of triangle CAD.
Similarly the triangles GAE and
CGE are also equal in area. This means that the area of triangle GAE =area of
triangle CGE =1/3 area of triangle CAD.
We can now conclude that the
triangles GAE, CGE, CAD and EAD are all equal in area. The rest of the proof is
trivial.
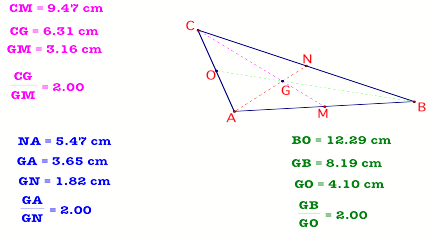
CONCURRENCY
Figure
4
From figure 4 we see two
important things
1. The medians are
concurrent.
2. The medians of a triangle
intersect each other in the ratio 2:1
Proof
There are a number of theorems
that we need to look at before we doing the proof. Here I will simply state the
theorems (formal proofs are omitted, but are part of secondary school
mathematics)
1. Mid-Segment theorem
A line joining the midpoints of two sides of a
triangle is parallel to the
third side and equal to half of it.
2. If a pair of opposite sides
are equal and parallel, the quadrilateral is a
parallelogram.
3. Diagonals of a parallelogram
bisect each other.
We start the proof as follows.
Construction: Let the three
medians meet in G. Let Q be the midpoint of GB, P the midpoint of AG, K the midpoint of CG
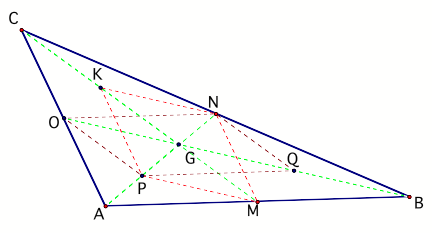
PROOF: PQ is parallel to AB and
also PQ=1/2 AB (mid segment theorem)
ON is parallel to AB and also ON=1/2 AB (mid segment theorem)
This means that PQ=ON and PQ is parallel to ON.
We can conclude here
that the quad OPQN is a parallelogram
(Theorem). Also we know that diagonals of a parallelogram bisect
each other. In this case PN intersects with OQ in G. We can also
argue that the median AN intersects with the median BO at G.
Using the same argument that we
used to show that OPQN is a parallelogram, we can show that KPMN is also a
parallelogram.
Similarly the diagonals of KPMN
intersect and bisect each other at the point G, also the median CM intersects
with the median BO in G.
From above we know that the
median BO intersects with the median AN in G, therefore G must be the common
point where all the three medians are meeting. So the three medians are
concurrent.
For us to show that the medians
intersect each other in the ratio 2:1, we can just use the results from above.
We have already proved that OPQM and KPMN are parallelograms.
We know also that diagonals of
a parallelogram bisect each other.
This means then that in
parallelogram OPQN, OG =GQ. But we also know through construction that GQ =QB.
Therefore OG=GQ=QB=1/3 OB. ( or BG=2/3OB)
Using the same argument we can
say that AP=PG=GN = 1/3 AN(or AG=2/3AN).
In the same manner we can show
that CG=2/3 CM.
The conclusion is therefore
that the medians of a triangle intersect each other in the ratio 2:1
Remember earlier on we had a
conjecture that when one median of a triangle is drawn the second median
divides the triangle formed by the first median in the ratio 1:2. Now we are
ready to write the proof:

We now know that the medians of
triangle intersect each other in the ratio 2:1. Let us consider the triangle
CDA. Our results show that its area is 3times the area of triangle GAD. These
triangles are sitting on the same base CD and share the same vertex ÒAÓ, so
they have the same altitude.
Area of triangle CAG = 1/2
CG times the altitude
Area of triangle GAD = 1/2 GD times the
altitude
= CG
GD
= 2/3 CD
1/3 CD
=2
1
NOTE: There are still a number of
things that can be explored
about
the medians of a triangle. Here I concentrated on the
areas
and concurrency.