ASSIGNMENT 9

BY

SHADRECK S CHITSONGA

PEDAL TRIANGLES

In most of the books of high school mathematics students are presented with different types of triangle. The majority of students are familiar with the following terms Isosceles triangle, right triangle, equilateral triangle, and scalene triangle. Very few students are familiar with the other classification of triangles. For example the orthic triangle, pedal triangle. In this write up I will focus on the pedal triangles.

There are different types of pedal triangles, and they have a number of interesting properties. We will discuss a few examples here. We will start by first of all looking at how different pedal triangles are formed.

1. Consider the following construction. A triangle ABC is constructed perpendiculars are drawn from each of the three vertices to the opposite side. The point where these perpendiculars meet is called the orthocenter. Let us call this point H. Bisect each of the following segments BH, AH, and CH. Let the mid points be E, F, D , respectively. The triangle EDF is called a pedal triangle.

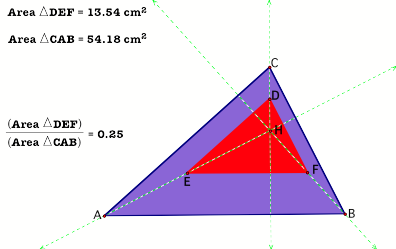
In can be shown that the area of triangle DEF will always have an area equal to quarter the area of the original triangle ABC.

Consider the triangle AHC, AF=FH and DH=DC (F and H are midpoints)

This means that DF is half the length of AC and also parallel to it. Similarly, DE=1/2 CB and also parallel, FE=1/2 AB and also parallel to it.

Therefore triangles DFE and ABC are similar. This means that:

DF = DE = FE

AB AC BC

It follows that the ratio Area of triangle DFE is 1

Area of triangle ABC 4

CLICK here to alter size of triangle ABC

2. Consider a triangle ABC with the sides produced. We can draw a triangle that connects the points of tangency of the escribed circles. See the diagram below the triangles IJK, DEF, JDH are pedal triangles. In this case the pedal points are the circumcenters of the triangles.

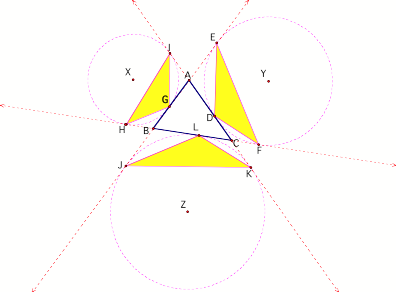
It can be shown that these triangles are always obtuse. Let us follow

the proof below. Consider one pedal triangle only.

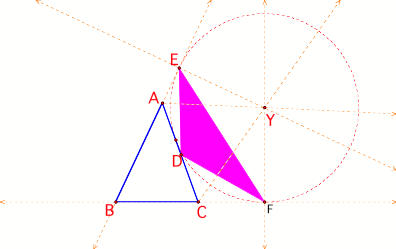
From Y we drop a perpendicular to meet BC produced in F.

BF and BE are tangents from an external point, therefore they are equal in length. This means that triangle BFE is an isosceles.

Angle BFE = angle BEF (base angles isosceles triangle)

But angle YFB = 90 degrees (radius perpendicular to tangent)

Similarly angle YEB =90 degrees.

It follows that angle BFD is less than 90 degrees therefore it is acute. Also EDB is acute.

Consider the tangents AD and AE, these are equal in length (tangents from an external point theorem)

Similarly CD and CF are also equal in length.

It follows then that angle AED = angle ADE, and angle CDF = DFC.

But angle DFC = angle DEF (alternate segment theorem)

Similarly angle EDB = angle EFD.

We know that angle EFC is than angle YFB therefore less than 90 degrees .

But angle EFC= angle EFD + angle DFC

= angle EFD + angle DEF

Angle EDF=180 degrees - (angle EFD + angle DEF)

>90 degrees since (angle EFD + angle DEF) is less than 90

degrees.

Therefore triangle EFD is obtuse.

3. Let ABC be any triangle. If P is any point in the plane, then the triangle formed by constructing the perpendiculars to the sides ABC, and locating the three intersections is the pedal triangle for the Pedal point P.

Here is the diagram

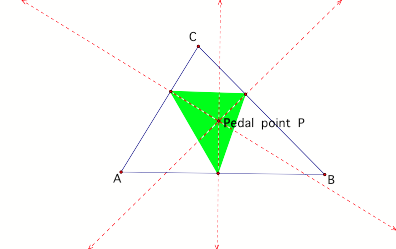
We will now focus our attention on the third one and explore a few things regarding the pedal point P. Remember P in (3) is just an arbitrary point. Let us look at a few special cases.

1. Let us consider the case when the pedal point P is the in center of the

triangle ABC.

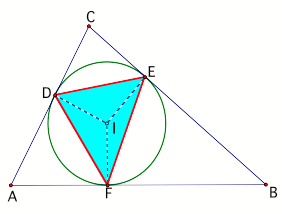
Triangle DEF is a pedal triangle. It can be shown that this triangle is always Isosceles. Here is the proof

By construction we can join ID,IF, and IE.

AF = AD, BF = BE, and CE = CD (tangents from an external point)

It follows that angle AFD = angle ADF, angle BFE = angle BEF,

angle CED = angle CDE (base angles of isosceles triangle are equal)

But angle IFA= angle IDC = angle IEC (radius perpendicular to tangent)

This means that each of the following angles AFD, DFI, IDC, CED, BEF and BFI is less than 90 degrees, therefore acute.

But angle AFD = angle DEF, angle BFE = angle FDE, and angle CDE = angle DFE (alternate segment theorem).

But the angles DEF, FDE, and DFE are the angles of triangle DFE and they are all acute.

Therefore triangle DFE is acute.

CLICK HERE to see what happens when you change the size of triangle ABC. Check whether any of the three angles of the pedal triangle becomes obtuse.