
Bouncing
Barney and Ceva's
Theorem
Final Assignment
by
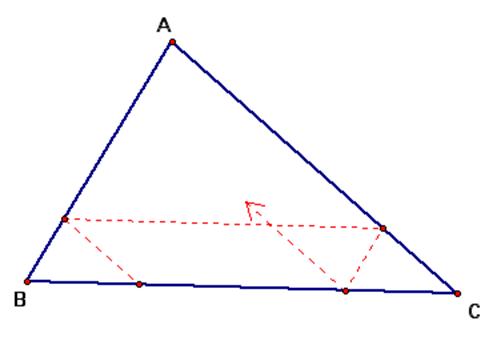
A. Barney is in the triangular
room shown here. He walks from a point on BC parallel to AC. When he reaches
AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks
parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall
before returning to his starting point? Explore
and discuss for various starting points on line BC, including points exterior
to segment BC. Discuss and prove any mathematical conjectures you find in the
situation.
Here
is a GSP file of Bouncing Barney (triangle with line segments). A script tool has been included in the download. Clickhere.
If
you want to look Barney’s exterior path (triangle with lines), click here for a GSP file with this script tool.
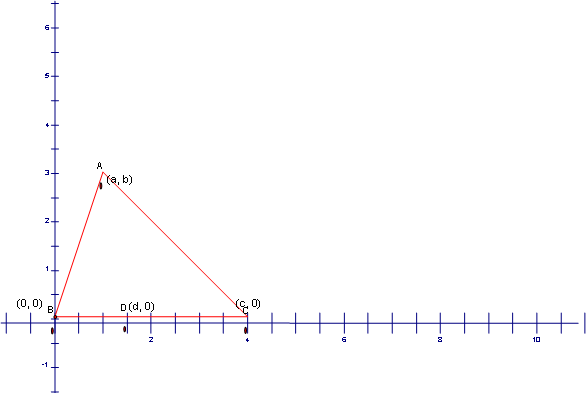
Let
us begin the proof that Barney will eventually return to his starting point by labeling
the triangle like shown below:
Algebraically,
line segment AB is the line y = a/b x, line segment AC is the line y = b/(a-c) x – bc/(a-c), and line
segment BC is the line y = 0. I will not
go through all the algebra but the first few steps. First, construct a line through (d,0), where Barney starts, parallel to AC and intersecting
AB. This line would have the same slope
as AC and goes through (d, 0). So the
equation of this line would be y = b/(a-c) (x-d). This line would intersect AB at the point
(ad/c, bd/c). This is the first leg of Barney’s
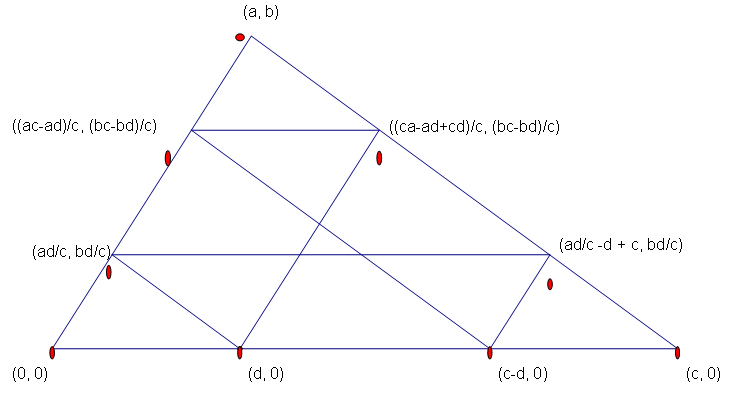
journey. The proof consists of 5 more
equations with intersections on the sides of the triangle as shown below:
Barney
turns 5 times with 6 legs back to the starting point.
What
about choosing a point exterior of the triangle?
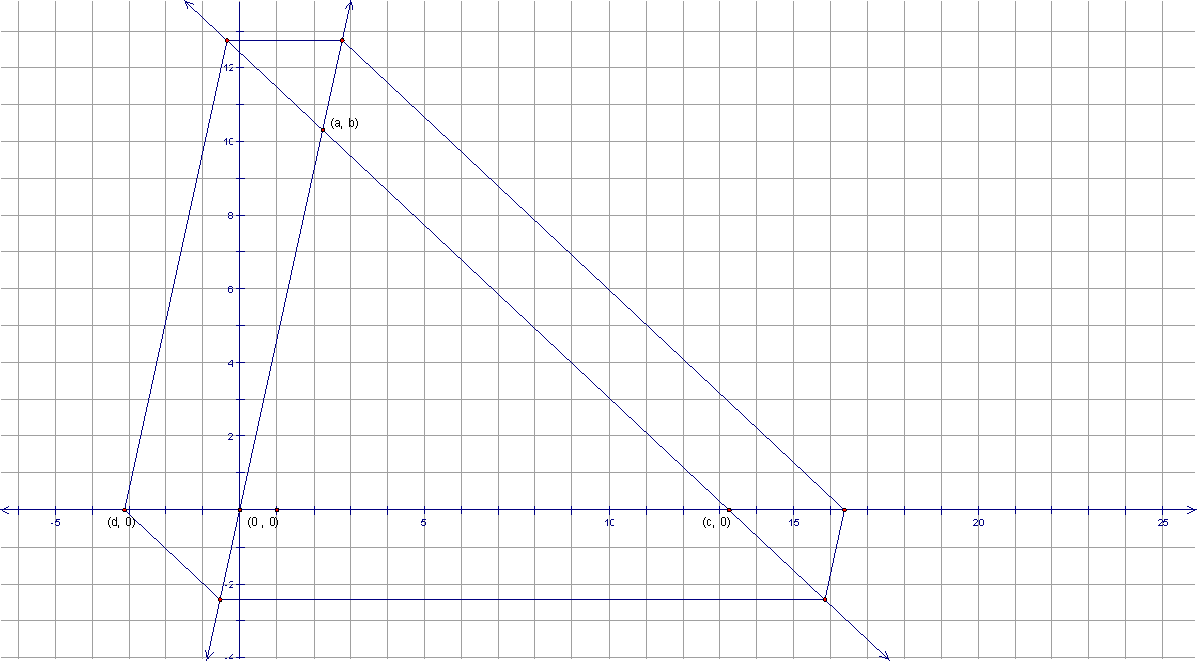
Notice
the Superman shield? Also, note that
Barney returns to his starting point with 5 turns and 6 legs of the journey
around the exterior of the triangle.
Barney
is located at (d, 0). The line segment
formed from the starting point (d, 0) to the intersection of line AC has an
equation y = b/a
(x-d) since it is parallel to line AB. Thus
the intersection point is
(a
+ c – ad/c, (abc – abd)/c(a – c)). Look
familiar? Similarly to the above
algebraic proof, we can conclude that Barney does make it back to (d, 0).
Conjecture: If Barney starts at a midpoint of one of the
sides of the triangle, he will have 2 turns to make and 3 legs of the journey
to make it back to his starting point. Also,
several similar triangles are formed.
Look at the picture below.
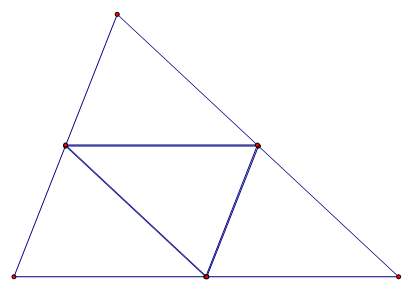
Conclusions:
1. Barney returns to his starting
point if walking inside or outside the triangle.
2. If Barney starts at the midpoint,
he returns after 2 turns to his starting point.
3. If Barney starts at any other
point on BC besides the midpoint, he returns after 5 turns to his starting
point.
4. Perimeter:
a. If Barney starts on a midpoint of
the side of the triangle, he will travel half of the triangle’s perimeter.
b. If Barney starts on any other
point besides the midpoint of a side of the triangle, he will travel the
triangle’s perimeter before returning to his starting point.
These
conclusions could be proved using properties of similar triangles (unlike the
algebraic proofs above).
B. Ceva's Theorem. Consider any
triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and
CP extended to their intersections with the opposite sides in points D, E, and
F respectively.
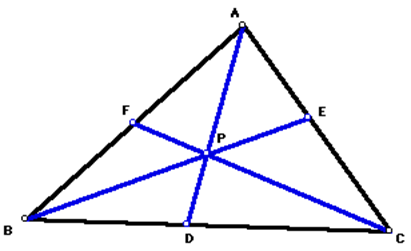
Exploration:
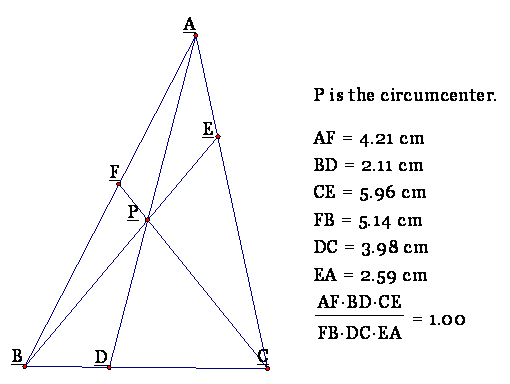
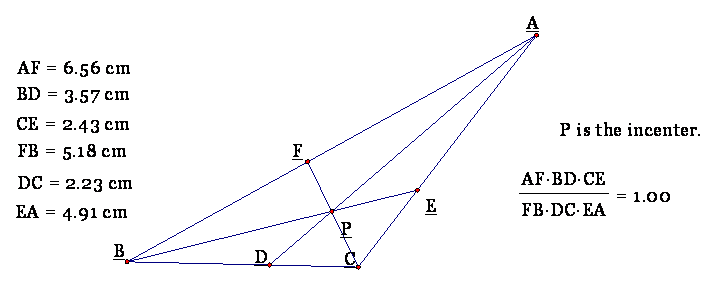
Consider the ratio
below in any triangle:
![]()
The above ratio is
equal to 1 if inside the triangle ABC.
For this proof, draw a
line through A
parallel to line segment BC as shown below.
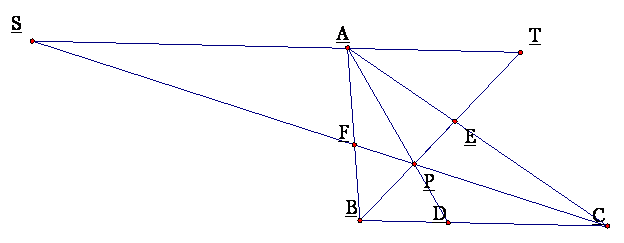
Constructing the line
segments above, several similar triangles are formed.
Δ AET ~ Δ CEB, so AE / EC = AT / CB. (I)
Δ BFC ~ Δ AFS, so BF / FA = CB / SA. (II)
Δ CDP ~ Δ SAP, so CD / SA = DP / AP. (III)
Δ BDP ~ Δ TAP, so BD / TA = DP / AP. (IV)
Looking at (III) and
(IV), CD / SA = BD / TA. With a little
algebra, this proportion is the same as CD / BD = SA / TA. (V)
By multiplying (I),
(II), (V), AE / EC * BF / FA * CD / DB = AT / CB * CB / SA * SA / TA = 1, or
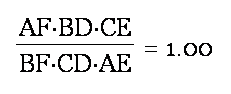
Conjectures:
1.
The
medians of any triangle are concurrent.
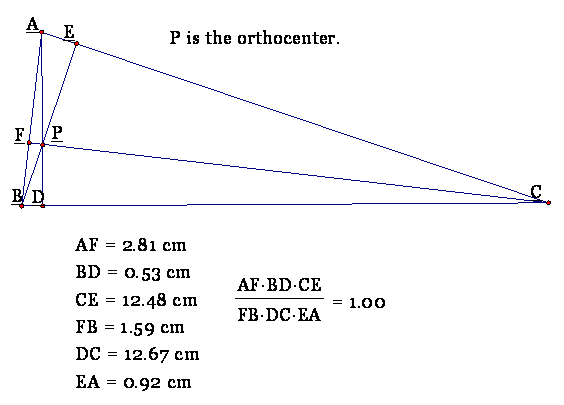
2.
The
altitudes of any triangle are concurrent.
3.
The
interior angle bisectors of a triangle are concurrent.
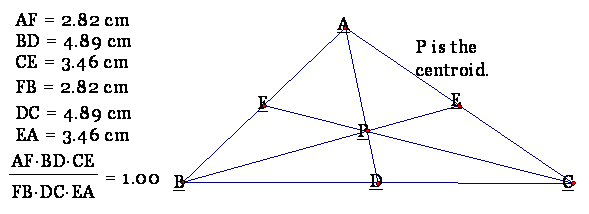
Let us look again at the centroid case:
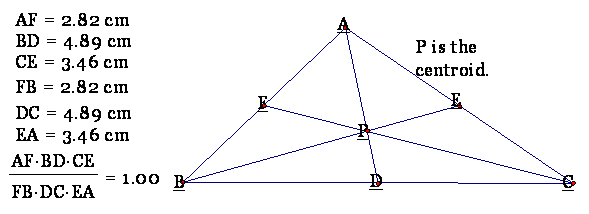
In triangle ABC, line
segments AD, BE, and CF are medians. Therefore,
AF = FB, BD = DC, and CE = EA.
So (AF)(BD)(CE) = (FB)(DC)(EA), or
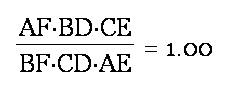
Thus, according to Ceva, line segments AD, BE, and CF are concurrent.
Exploration of Ceva’s
Theorem using lines rather than segments to construct ABC so that point P can
be outside the triangle. Below are sketches
of when the points P, D, E, and F are collinear.


According
to Menelaus, if we were to take direction into account in the two figures above
then the ratio would equal -1
instead of 1.
Click here to open a GSP file with the collinear cases
above.