
Exploration of Quadratic
(as b varies)
by
Chad Crumley
This exploration is about the graphs of
quadratic equations of the form.![]()
For this exploration, we are going to fix 2
of the values in the quadratic (a,
b, c) and see what conclusions can be found.
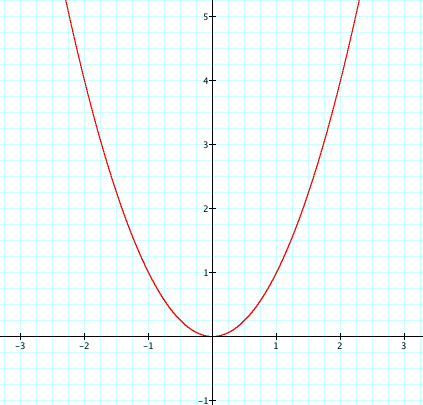
Before we begin, let's look at the parent
graph![]() .
.
Here is a movie
to see the changes in the quadratic equations with a=1, c = 1, and b varies
from -10 to 10 in one hundred steps. Click here.
Here is a graph
of 9 quadratic equations with a=1, c=1, and b = 0 (red), b = 1 (purple), b = 2
(blue), b = -2 (green), b = -1 (aqua), b = -0.5 (yellow), b = 0.5 (grey), b =
-3 (black), b = 3 (purple).
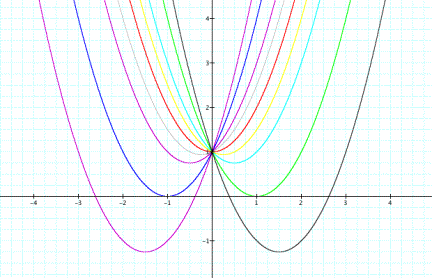
With varying the
b value in the quadratic
equation, it appears that the graph moves in a parabolic path.
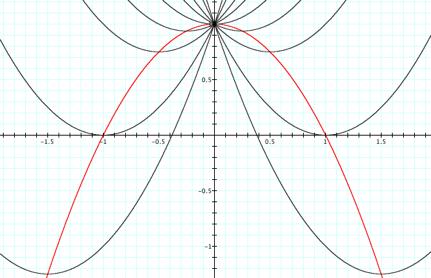
The graph above
is the same as the colorful graph above it. The only thing I did was made all of the equations in the
colorful graph black and graph the parabolic path in red,
which is y = -x2 +1.
Interesting! Here is another graph of different
quadratic equations in black and the parabolic path in red.
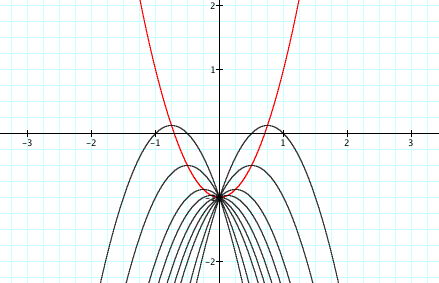
For the black graphs, a = -2 and c =-1 with b = -3,
-2, -1, -0.5, 0, 0.5, 1, 2, 3.
For the red graph, the parabolic path satisfies y = 2x2 -1.
Thus,
it appears that the parabolic path will always be the opposite of the a value given, b = 0, and the same c value
given.
Question: Given the quadratic equation, y = -0.5x2 + bx - 4. What
would be the parabolic path?
Click
here for a movie.
Conclusion: y
= 0.5x2 -4