
Exploration of the
centroid of a triangle
(Using Geometers
Sketchpad)
by
Chad Crumley
First, begin by constructing a triangle.
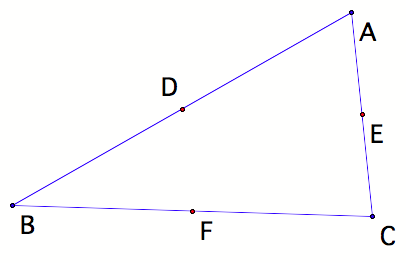
Then, construct the midpoints of all the sides.
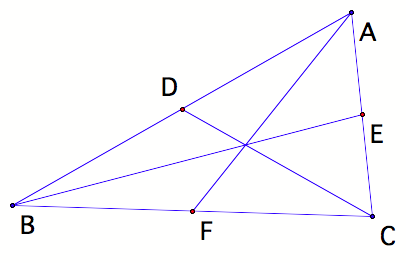
Now construct segments from each vertex to the midpoint on the opposite
side. For example, construct
segment BE. These segments are
called medians.
Finally, construct and label the intersection of the
newly constructed segments (or medians).
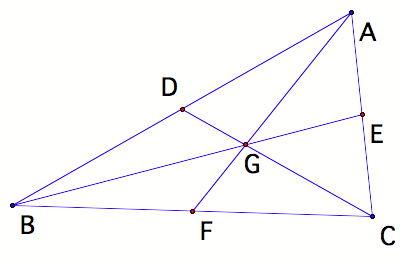
Point G is the centroid!
Here are some interesting relationships:
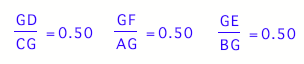
In words, given any median in a triangle, the distance
from the midpoint of the opposite side of a vertex to the centroid to the
distance from the vertex to the centroid will always be 1 to 2.
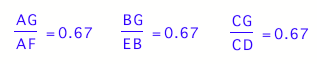
This means that the length of the longer piece of the
median (the side that is from any vertex to the centroid) to the length of the
entire median will always form a 2 to 3 correspondence.
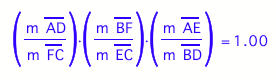
The relationship above looks scary, right? What does it mean? Thanks to Newton, this confirms that
the centroid is the center of gravity (aka the center of mass). Given any triangle, the triangle can be
balanced on its centroid (the intersection point of a its medians).
For exploration purposes, here is a GSP script tool
that creates the centroid of a triangle.
Click here.