Football Problem
by
Chad Crumley
The football
rules in college football were changed a few years ago made the uprights 5 feet
narrower than previously. Many game commentators have harped about how much harder
it is to kick field goals from the hash marks. Assume the field goal is
attempted from the hash marks. At what yard marker does the kicker have maximum
angle to the two uprights. Note: You will need to find out the width of the
uprights and the width of the hash marks . . . make a sketchpad model. Is there
any merit to some commentatorsŐ argument to take a penalty in order to have a
"better angle" on the field goal kick?
Here is a GSP representation of a collegiate football
field:
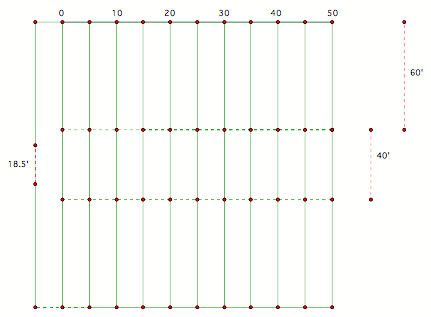
Let us investigate the largest angle by making a point
on one of the hash marks (the top one) and connecting segments to the sides of
the upright (<DOG).
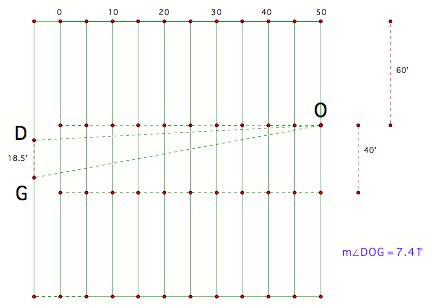
Let us do some measurements. Below you can see an angle of 7.41 degrees is formed when
placing the ball on the 50-yard line.
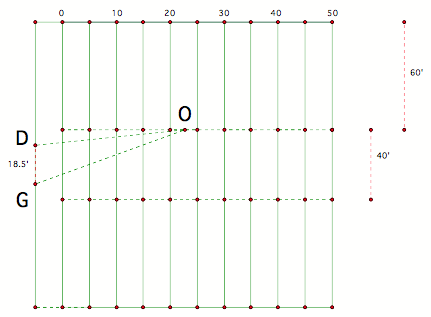
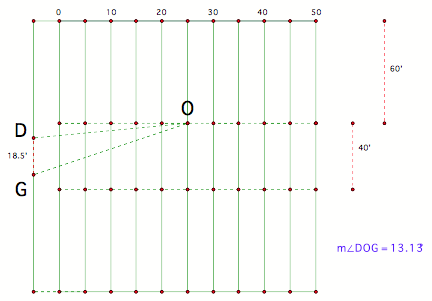
What
about the 25-yard line? An angle
of 13.13 degrees is formed. This
angle is larger and increases the probability of kicking the football through
the uprights.
Here is the angle formed when kicking the football at
the 10-yard line.
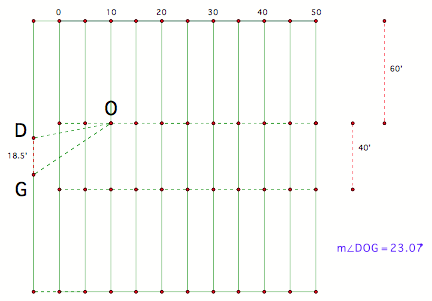
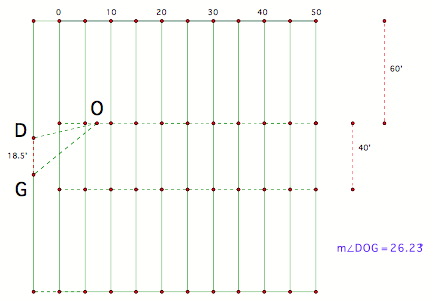
Notice <DOG keeps getting better. So, to answer the question, the commentators
need to do some geometry explorations like above. The team should not take any penalty to better the
angle. The maximum angle would be
reached at the 7-yard line (which is where kicker attempts the extra point). <DOG measures about 26 degrees.