
Altitudes and Orthocenters
by
Chad Crumley
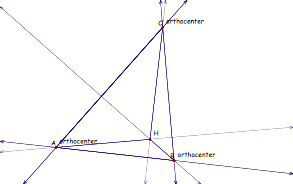
1. Construct
any triangle ABC.
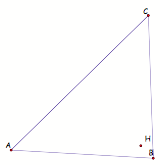
2. Construct
the Orthocenter H of triangle ABC.
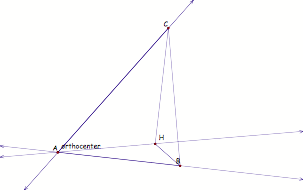
3. Construct
the Orthocenter of triangle HBC.
4. Construct the
Orthocenter of triangle HAB.
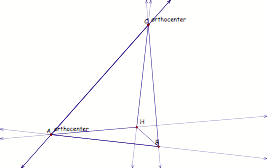
5. Construct
the Orthocenter of triangle HAC.
6. Construct
the Circumcircles of triangles ABC, HBC, HAB, and HAC.
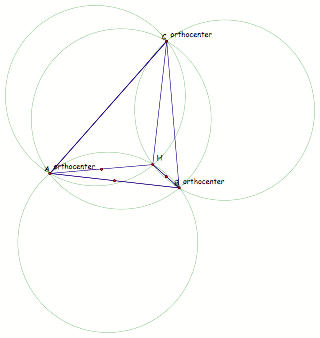
7.
Conjectures?
a. Just from viewing the object above, it
appears that all of the circumcircles have the same area (or radius). A proof of this could include congruent arcs through 2
points, eventually going around triangle ABC and including all parts of the 4
circumcircles.
b. The orthocenters of triangles AHB, BHC,
CHA lie on the vertices of triangle ABC (a proof by contradiction may be best
in this case).