Pedal Triangle Exploration
by
Chad Crumley
This is an
investigation of merging the pedal point to different centers of a given
triangle.
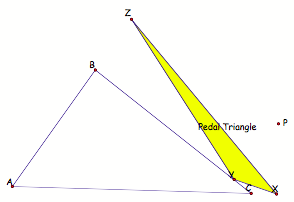
First, here is
triangle ABC with its pedal triangle XYZ and pedal point P.
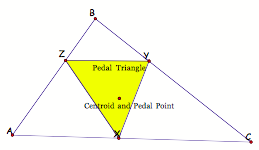
- What happens when the pedal
point merges with the centroid of triangle ABC?
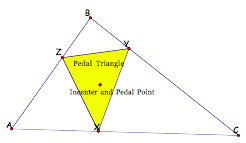
2.
What happens when the pedal point merges with the incenter of triangle
ABC?
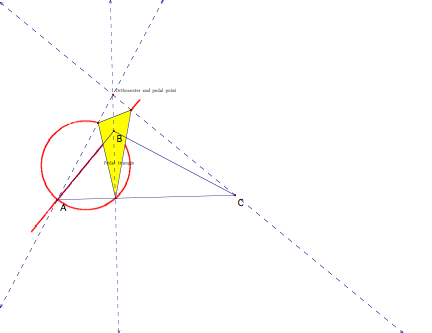
- What happens when the pedal
point merges with the orthocenter of triangle ABC (inside)?
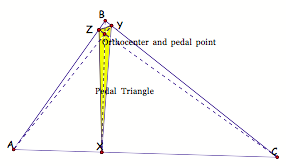
- What happens when the pedal point
merges with the orthocenter of triangle ABC (outside)?

Conclusion: It appears that for #1, 2, and 3 the
vertices of the pedal triangle will lie on the given triangle ABC. For #3 and 4, it appears that the
vertices of the pedal triangle will lie on the altitudes of the given triangle
ABC, regardless of the orthocenter being inside or outside triangle ABC.
What happens when the
pedal point lies on a vertex of triangle ABC? Click here to explore.
What happens if you
trace the vertices of the pedal triangle while moving a vertex of the original
triangle? Click
here to explore. The trace
leaves a circle and a line through the circle. Two vertices of the pedal triangle are always on the circle. Did you get something like this?