EMAT 6690: Using Computers in Mathematics Instruction
Dr. J. Wilson, Instructor
Using Computers to Conjecture Solutions to Contextual Teaching & Learning Problems
An Essay by Ryan Fox
My goal in creating this essay was to take a group of three problems from the Contextual Teaching & Learning (CTL) website and implement computer software programs to help facilitate solutions to these three problems. It was my hope that as I was completing these solutions, I would not only use computer software, but also use methods that are basic enough for secondary students could understand and duplicate. The problems from CTL emphasize the practical application of mathematics to the real world setting. Using computer software programs brings an additional aspect to practical application.
First Investigation: Coins
Problem: In how many ways
can 19 coins equal exactly one dollar?
We can use the Microsoft Excel spreadsheet program to facilitate the studentÕs ability to guess and check potential solutions to the problem. This is an example of the results that the spreadsheet can generate. (A link to the spreadsheet can also be found here.)
|
Pennies |
Nickels |
Dimes |
Quarters |
Half-Dollars |
Coins |
|
Value |
|
15 |
2 |
|
1 |
1 |
19 |
Success! |
1 |
|
5 |
12 |
1 |
1 |
|
19 |
Success! |
1 |
|
10 |
6 |
1 |
2 |
|
19 |
Success! |
1 |
|
15 |
|
1 |
3 |
|
19 |
Success! |
1 |
|
10 |
8 |
|
|
1 |
19 |
Success! |
1 |
|
10 |
|
9 |
|
|
19 |
Success! |
1 |
|
|
18 |
1 |
|
|
19 |
Success! |
1 |
|
5 |
4 |
|
1 |
1 |
11 |
Failure |
1 |
|
4 |
14 |
|
1 |
|
19 |
Failure |
0.99 |
|
5 |
4 |
5 |
1 |
|
15 |
Failure |
1 |
|
5 |
10 |
2 |
1 |
|
18 |
Failure |
1 |
|
5 |
8 |
3 |
1 |
|
17 |
Failure |
1 |
|
5 |
13 |
|
1 |
|
19 |
Failure |
0.95 |
|
10 |
1 |
6 |
1 |
|
18 |
Failure |
1 |
|
10 |
7 |
|
2 |
|
19 |
Failure |
0.95 |
|
10 |
2 |
3 |
2 |
|
17 |
Failure |
1 |
|
15 |
2 |
|
2 |
|
19 |
Failure |
0.75 |
|
10 |
4 |
2 |
2 |
|
18 |
Failure |
1 |
|
|
13 |
1 |
1 |
|
15 |
Failure |
1 |
|
5 |
9 |
|
|
1 |
15 |
Failure |
1 |
|
5 |
5 |
2 |
|
1 |
13 |
Failure |
1 |
|
10 |
|
4 |
|
1 |
15 |
Failure |
1 |
|
5 |
14 |
|
|
|
19 |
Failure |
0.75 |
|
5 |
7 |
1 |
|
1 |
14 |
Failure |
1 |
|
5 |
9 |
|
2 |
|
16 |
Failure |
1 |
|
10 |
|
4 |
2 |
|
16 |
Failure |
1 |
|
10 |
1 |
1 |
3 |
|
15 |
Failure |
1 |
In this spreadsheet, we used five different coins: pennies (1¢), nickels (5¢), dimes (10¢), quarters (25¢), and half-dollars (50¢). While students may not be familiar with the half-collar coin, the inclusion of this coin allows the student to come up with additional possibilities. This leads to the idea that if there were other coins in circulation, then there could be additional correct combinations that lead to a dollar.
This spreadsheet sets up a few equations in order for the students to conjecture rapidly without having to work on the calculations. There are three equations that are set up in this spreadsheet. In the sixth column, we have added the number of coins that the student has put in the spreadsheet. In the eighth column, we have determined the value of the coins that the students have put together. If both conditions are met (19 coins that have a value of one dollar), then the entry in the seventh column will display the word ÒSuccess!Ó As the students begin to put in numbers into one row, the number of coins and the value of those coins will change. Once the student matches both conditions, then the word ÒSuccess!Ó appears.
Based on my work on the spreadsheet, I did find seven solutions to the problem. This spreadsheet will not be able to determine if the student has created an exhaustive list of solutions, only that the conjectures the students are correct or not.
Second Investigation: Arithmetic Mean Sequence
Problem: Given two numbers, a1 and a2,
define a sequence of terms such that for any term ak (where k is a
natural number), we can define ak by its two previous terms: ![]() , where k ³ 3. Does the sequence converge, and, if so,
to what value does it converge?
, where k ³ 3. Does the sequence converge, and, if so,
to what value does it converge?
Solution Path: To facilitate my work towards a solution, I used the GeometerÕs Sketchpad program and created two points with coordinates (0, 0) and (10,0). I chose these two points because I felt I could find the pattern more rapidly than any other selection of points. Once I plotted the points, I took the midpoint of the segment that connects (0, 0) and (10, 0), and measured the abscissa (x-coordinate) of the midpoint. I found the midpoint has an abscissa of 5. I then took the midpoint of the segment with endpoints (5, 0) and (10, 0). This midpoint has an abscissa of 7.5. I repeated the process repeatedly to get a sequence of abscissa to try to develop a pattern. The resulting abscissas were 6.25, 6.88, 6.56, 6.72, 6.64, 6.68, 6.66, 6.67, etc. I conjecture that the sequence does converge and that limit of the sequence is 2/3 the length of the segment.
I noticed that in the notes to this problem that clues were given that the if given the first two numbers of 3 and 6, then this particular sequence converges to 5. In my conjecture I would observe that the length of the segment is 3 units, and thus 2/3 of the length would be 2 units. Unlike the previous instance, we need to add the 2/3 length to the lower of the original numbers; thus 3 + 2 = 5. The answer arrived at here matches the answer given in the notes. Likewise, if given the first two numbers as 1 and 10, we could find that the length of this segment is 9 and thus 2/3 of the length of this segment is 6 units. Adding 6 to the value of the lower of the two original numbers yields 1 + 6 = 7. The value obtained from this conjecture yields the same value provided in the notes.
At this point, I would say that the sequence does indeed
converge and the limit of the sequence is ![]() , using the notation from the beginning of the problem.
, using the notation from the beginning of the problem.
Alternate Solution Path: We could use spreadsheets to
provide additional insight to this problem. We can create a formula for the arithmetic mean of the two
numbers and we can generate that second number by referring to the arithmetic mean
of the previous two terms.
Examples of the previous three situations are given below in spreadsheet
form.
|
First |
Second |
A. Mean |
First |
Second |
A. Mean |
First |
Second |
A. Mean |
|
0 |
10 |
5 |
3 |
6 |
4.5 |
1 |
10 |
5.5 |
|
10 |
5 |
7.5 |
6 |
4.5 |
5.25 |
10 |
5.5 |
7.75 |
|
5 |
7.5 |
6.25 |
4.5 |
5.25 |
4.875 |
5.5 |
7.75 |
6.625 |
|
7.5 |
6.25 |
6.875 |
5.25 |
4.875 |
5.0625 |
7.75 |
6.625 |
7.1875 |
|
6.25 |
6.875 |
6.5625 |
4.875 |
5.0625 |
4.96875 |
6.625 |
7.1875 |
6.90625 |
|
6.875 |
6.5625 |
6.71875 |
5.0625 |
4.96875 |
5.015625 |
7.1875 |
6.90625 |
7.046875 |
|
6.5625 |
6.71875 |
6.640625 |
4.96875 |
5.015625 |
4.9921875 |
6.90625 |
7.046875 |
6.9765625 |
|
6.71875 |
6.640625 |
6.6796875 |
5.015625 |
4.9921875 |
5.00390625 |
7.046875 |
6.9765625 |
7.01171875 |
|
6.640625 |
6.6796875 |
6.66015625 |
4.9921875 |
5.00390625 |
4.998046875 |
6.9765625 |
7.01171875 |
6.994140625 |
|
6.6796875 |
6.66015625 |
6.669921875 |
5.00390625 |
4.998046875 |
5.000976563 |
7.01171875 |
6.994140625 |
7.002929688 |
|
6.66015625 |
6.669921875 |
6.665039063 |
4.998046875 |
5.000976563 |
4.999511719 |
6.994140625 |
7.002929688 |
6.998535156 |
|
6.669921875 |
6.665039063 |
6.667480469 |
5.000976563 |
4.999511719 |
5.000244141 |
7.002929688 |
6.998535156 |
7.000732422 |
|
6.665039063 |
6.667480469 |
6.666259766 |
4.999511719 |
5.000244141 |
4.99987793 |
6.998535156 |
7.000732422 |
6.999633789 |
|
6.667480469 |
6.666259766 |
6.666870117 |
5.000244141 |
4.99987793 |
5.000061035 |
7.000732422 |
6.999633789 |
7.000183105 |
|
6.666259766 |
6.666870117 |
6.666564941 |
4.99987793 |
5.000061035 |
4.999969482 |
6.999633789 |
7.000183105 |
6.999908447 |
|
6.666870117 |
6.666564941 |
6.666717529 |
5.000061035 |
4.999969482 |
5.000015259 |
7.000183105 |
6.999908447 |
7.000045776 |
|
6.666564941 |
6.666717529 |
6.666641235 |
4.999969482 |
5.000015259 |
4.999992371 |
6.999908447 |
7.000045776 |
6.999977112 |
|
6.666717529 |
6.666641235 |
6.666679382 |
5.000015259 |
4.999992371 |
5.000003815 |
7.000045776 |
6.999977112 |
7.000011444 |
|
6.666641235 |
6.666679382 |
6.666660309 |
4.999992371 |
5.000003815 |
4.999998093 |
6.999977112 |
7.000011444 |
6.999994278 |
|
6.666679382 |
6.666660309 |
6.666669846 |
5.000003815 |
4.999998093 |
5.000000954 |
7.000011444 |
6.999994278 |
7.000002861 |
|
6.666660309 |
6.666669846 |
6.666665077 |
4.999998093 |
5.000000954 |
4.999999523 |
6.999994278 |
7.000002861 |
6.999998569 |
|
6.666669846 |
6.666665077 |
6.666667461 |
5.000000954 |
4.999999523 |
5.000000238 |
7.000002861 |
6.999998569 |
7.000000715 |
|
6.666665077 |
6.666667461 |
6.666666269 |
4.999999523 |
5.000000238 |
4.999999881 |
6.999998569 |
7.000000715 |
6.999999642 |
|
6.666667461 |
6.666666269 |
6.666666865 |
5.000000238 |
4.999999881 |
5.00000006 |
7.000000715 |
6.999999642 |
7.000000179 |
|
6.666666269 |
6.666666865 |
6.666666567 |
4.999999881 |
5.00000006 |
4.99999997 |
6.999999642 |
7.000000179 |
6.999999911 |
|
6.666666865 |
6.666666567 |
6.666666716 |
5.00000006 |
4.99999997 |
5.000000015 |
7.000000179 |
6.999999911 |
7.000000045 |
|
6.666666567 |
6.666666716 |
6.666666642 |
4.99999997 |
5.000000015 |
4.999999993 |
6.999999911 |
7.000000045 |
6.999999978 |
|
6.666666716 |
6.666666642 |
6.666666679 |
5.000000015 |
4.999999993 |
5.000000004 |
7.000000045 |
6.999999978 |
7.000000011 |
|
6.666666642 |
6.666666679 |
6.66666666 |
4.999999993 |
5.000000004 |
4.999999998 |
6.999999978 |
7.000000011 |
6.999999994 |
|
6.666666679 |
6.66666666 |
6.66666667 |
5.000000004 |
4.999999998 |
5.000000001 |
7.000000011 |
6.999999994 |
7.000000003 |
|
6.66666666 |
6.66666667 |
6.666666665 |
4.999999998 |
5.000000001 |
5 |
6.999999994 |
7.000000003 |
6.999999999 |
|
6.66666667 |
6.666666665 |
6.666666667 |
5.000000001 |
5 |
5 |
7.000000003 |
6.999999999 |
7.000000001 |
|
6.666666665 |
6.666666667 |
6.666666666 |
5 |
5 |
5 |
6.999999999 |
7.000000001 |
7 |
|
6.666666667 |
6.666666666 |
6.666666667 |
5 |
5 |
5 |
7.000000001 |
7 |
7 |
|
6.666666666 |
6.666666667 |
6.666666667 |
5 |
5 |
5 |
7 |
7 |
7 |
Using spreadsheets would be even more useful if for solving
the extension problems.
Extension Problem: Given two numbers, a1
and a2, define a sequence of terms such that for any term ak
(where k is a natural number), we can define ak by its two previous
terms: ![]() , where k ³ 3. Does the sequence converge, and, if so,
to what value does it converge?
, where k ³ 3. Does the sequence converge, and, if so,
to what value does it converge?
Solution Path: In this problem, using the Spreadsheet
program could facilitate the work towards a solution. If we keep the same
values from the earlier problem, but change the arithmetic mean to the
geometric mean, we could see a possible solution to this particular problem.
|
First |
Second |
G. Mean |
First |
Second |
G. Mean |
First |
Second |
G. Mean |
|
9 |
16 |
12 |
3 |
6 |
4.242640687 |
1 |
10 |
3.16227766 |
|
16 |
12 |
13.85640646 |
6 |
4.242640687 |
5.045378492 |
10 |
3.16227766 |
5.623413252 |
|
12 |
13.85640646 |
12.89483918 |
4.242640687 |
5.045378492 |
4.626632476 |
3.16227766 |
5.623413252 |
4.216965034 |
|
13.85640646 |
12.89483918 |
13.3669792 |
5.045378492 |
4.626632476 |
4.831470996 |
5.623413252 |
4.216965034 |
4.869675252 |
|
12.89483918 |
13.3669792 |
13.12878696 |
4.626632476 |
4.831470996 |
4.727942535 |
4.216965034 |
4.869675252 |
4.531583638 |
|
13.3669792 |
13.12878696 |
13.24734774 |
4.831470996 |
4.727942535 |
4.779426454 |
4.869675252 |
4.531583638 |
4.697588817 |
|
13.12878696 |
13.24734774 |
13.18793412 |
4.727942535 |
4.779426454 |
4.753614796 |
4.531583638 |
4.697588817 |
4.613839683 |
|
13.24734774 |
13.18793412 |
13.21760755 |
4.779426454 |
4.753614796 |
4.766503153 |
4.697588817 |
4.613839683 |
4.655525931 |
|
13.18793412 |
13.21760755 |
13.2027625 |
4.753614796 |
4.766503153 |
4.760054612 |
4.613839683 |
4.655525931 |
4.634635939 |
|
13.21760755 |
13.2027625 |
13.21018294 |
4.766503153 |
4.760054612 |
4.763277791 |
4.655525931 |
4.634635939 |
4.645069192 |
|
13.2027625 |
13.21018294 |
13.2064722 |
4.760054612 |
4.763277791 |
4.761665929 |
4.634635939 |
4.645069192 |
4.639849633 |
|
13.21018294 |
13.2064722 |
13.20832744 |
4.763277791 |
4.761665929 |
4.762471792 |
4.645069192 |
4.639849633 |
4.642458679 |
|
13.2064722 |
13.20832744 |
13.20739979 |
4.761665929 |
4.762471792 |
4.762068844 |
4.639849633 |
4.642458679 |
4.641153972 |
|
13.20832744 |
13.20739979 |
13.2078636 |
4.762471792 |
4.762068844 |
4.762270314 |
4.642458679 |
4.641153972 |
4.64180628 |
|
13.20739979 |
13.2078636 |
13.20763169 |
4.762068844 |
4.762270314 |
4.762169577 |
4.641153972 |
4.64180628 |
4.641480114 |
|
13.2078636 |
13.20763169 |
13.20774765 |
4.762270314 |
4.762169577 |
4.762219945 |
4.64180628 |
4.641480114 |
4.641643194 |
|
13.20763169 |
13.20774765 |
13.20768967 |
4.762169577 |
4.762219945 |
4.762194761 |
4.641480114 |
4.641643194 |
4.641561654 |
|
13.20774765 |
13.20768967 |
13.20771866 |
4.762219945 |
4.762194761 |
4.762207353 |
4.641643194 |
4.641561654 |
4.641602424 |
|
13.20768967 |
13.20771866 |
13.20770416 |
4.762194761 |
4.762207353 |
4.762201057 |
4.641561654 |
4.641602424 |
4.641582039 |
|
13.20771866 |
13.20770416 |
13.20771141 |
4.762207353 |
4.762201057 |
4.762204205 |
4.641602424 |
4.641582039 |
4.641592231 |
|
13.20770416 |
13.20771141 |
13.20770779 |
4.762201057 |
4.762204205 |
4.762202631 |
4.641582039 |
4.641592231 |
4.641587135 |
|
13.20771141 |
13.20770779 |
13.2077096 |
4.762204205 |
4.762202631 |
4.762203418 |
4.641592231 |
4.641587135 |
4.641589683 |
|
13.20770779 |
13.2077096 |
13.20770869 |
4.762202631 |
4.762203418 |
4.762203025 |
4.641587135 |
4.641589683 |
4.641588409 |
|
13.2077096 |
13.20770869 |
13.20770915 |
4.762203418 |
4.762203025 |
4.762203221 |
4.641589683 |
4.641588409 |
4.641589046 |
|
13.20770869 |
13.20770915 |
13.20770892 |
4.762203025 |
4.762203221 |
4.762203123 |
4.641588409 |
4.641589046 |
4.641588727 |
|
13.20770915 |
13.20770892 |
13.20770903 |
4.762203221 |
4.762203123 |
4.762203172 |
4.641589046 |
4.641588727 |
4.641588887 |
|
13.20770892 |
13.20770903 |
13.20770898 |
4.762203123 |
4.762203172 |
4.762203148 |
4.641588727 |
4.641588887 |
4.641588807 |
|
13.20770903 |
13.20770898 |
13.20770901 |
4.762203172 |
4.762203148 |
4.76220316 |
4.641588887 |
4.641588807 |
4.641588847 |
|
13.20770898 |
13.20770901 |
13.20770899 |
4.762203148 |
4.76220316 |
4.762203154 |
4.641588807 |
4.641588847 |
4.641588827 |
|
13.20770901 |
13.20770899 |
13.207709 |
4.76220316 |
4.762203154 |
4.762203157 |
4.641588847 |
4.641588827 |
4.641588837 |
|
13.20770899 |
13.207709 |
13.20770899 |
4.762203154 |
4.762203157 |
4.762203155 |
4.641588827 |
4.641588837 |
4.641588832 |
|
13.207709 |
13.20770899 |
13.207709 |
4.762203157 |
4.762203155 |
4.762203156 |
4.641588837 |
4.641588832 |
4.641588834 |
|
13.20770899 |
13.207709 |
13.207709 |
4.762203155 |
4.762203156 |
4.762203156 |
4.641588832 |
4.641588834 |
4.641588833 |
|
13.207709 |
13.207709 |
13.207709 |
4.762203156 |
4.762203156 |
4.762203156 |
4.641588834 |
4.641588833 |
4.641588834 |
|
13.207709 |
13.207709 |
13.207709 |
4.762203156 |
4.762203156 |
4.762203156 |
4.641588833 |
4.641588834 |
4.641588834 |
From this spreadsheet, it seems that the sequences converge,
but it is difficult to determine the value of the convergence simply by looking
at the values of the spreadsheet. It
might take a little work to determine a relationship between the value of the
limit of convergence and the first two terms. If we make an analogy to the arithmetic mean problem, we
know that the subtraction is the inverse operation of addition and
multiplication represents repeated addition, and thus a conjecture to the
formula for the limit of convergence could be ![]() , because division is the inverse operation of multiplication
and exponents represents repeated multiplication.
, because division is the inverse operation of multiplication
and exponents represents repeated multiplication.
Extension Problem #2: Given
two numbers, a1 and a2, define a sequence of terms such
that for any term ak (where k is a natural number), we can define ak
by its two previous terms: ![]() ,
where k ³ 3. Does the sequence converge, and, if so, to what value does
it converge?
,
where k ³ 3. Does the sequence converge, and, if so, to what value does
it converge?
Solution Path: We could once again use the spreadsheet program to determine a possible convergence and a limit to that convergence.
|
First |
Second |
H. Mean |
First |
Second |
H. Mean |
First |
Second |
H. Mean |
|
9 |
16 |
0.086805556 |
3 |
6 |
0.25 |
1 |
10 |
0.55 |
|
16 |
0.086805556 |
5.79125 |
6 |
0.25 |
2.083333333 |
10 |
0.55 |
0.959090909 |
|
0.086805556 |
5.79125 |
5.846337147 |
0.25 |
2.083333333 |
2.24 |
0.55 |
0.959090909 |
1.430417923 |
|
5.79125 |
5.846337147 |
0.171860781 |
2.083333333 |
2.24 |
0.463214286 |
0.959090909 |
1.430417923 |
0.870875207 |
|
5.846337147 |
0.171860781 |
2.994855231 |
2.24 |
0.463214286 |
1.302628318 |
1.430417923 |
0.870875207 |
0.923683265 |
|
0.171860781 |
2.994855231 |
3.076284575 |
0.463214286 |
1.302628318 |
1.463253377 |
0.870875207 |
0.923683265 |
1.115446168 |
|
2.994855231 |
3.076284575 |
0.329486706 |
1.302628318 |
1.463253377 |
0.725543665 |
0.923683265 |
1.115446168 |
0.989562221 |
|
3.076284575 |
0.329486706 |
1.680045636 |
1.463253377 |
0.725543665 |
1.03084272 |
1.115446168 |
0.989562221 |
0.953525063 |
|
0.329486706 |
1.680045636 |
1.815122872 |
0.725543665 |
1.03084272 |
1.174178446 |
0.989562221 |
0.953525063 |
1.029644003 |
|
1.680045636 |
1.815122872 |
0.573074409 |
1.03084272 |
1.174178446 |
0.910869699 |
0.953525063 |
1.029644003 |
1.009974797 |
|
1.815122872 |
0.573074409 |
1.147950495 |
1.174178446 |
0.910869699 |
0.974755587 |
1.029644003 |
1.009974797 |
0.98066659 |
|
0.573074409 |
1.147950495 |
1.308045902 |
0.910869699 |
0.974755587 |
1.061875033 |
1.009974797 |
0.98066659 |
1.004919138 |
|
1.147950495 |
1.308045902 |
0.817808435 |
0.974755587 |
1.061875033 |
0.983814299 |
0.98066659 |
1.004919138 |
1.007409751 |
|
1.308045902 |
0.817808435 |
0.993639706 |
1.061875033 |
0.983814299 |
0.979091194 |
1.004919138 |
1.007409751 |
0.993874846 |
|
0.817808435 |
0.993639706 |
1.114590627 |
0.983814299 |
0.979091194 |
1.018903654 |
1.007409751 |
0.993874846 |
0.999403827 |
|
0.993639706 |
1.114590627 |
0.951795699 |
0.979091194 |
1.018903654 |
1.001401192 |
0.993874846 |
0.999403827 |
1.003379716 |
|
1.114590627 |
0.951795699 |
0.973918015 |
1.018903654 |
1.001401192 |
0.990023916 |
0.999403827 |
1.003379716 |
0.998614099 |
|
0.951795699 |
0.973918015 |
1.038713056 |
1.001401192 |
0.990023916 |
1.004338689 |
1.003379716 |
0.998614099 |
0.999009746 |
|
0.973918015 |
1.038713056 |
0.99475513 |
0.990023916 |
1.004338689 |
1.002878332 |
0.998614099 |
0.999009746 |
1.00118953 |
|
1.038713056 |
0.99475513 |
0.984001156 |
1.004338689 |
1.002878332 |
0.996404992 |
0.999009746 |
1.00118953 |
0.999901559 |
|
0.99475513 |
0.984001156 |
1.010765746 |
1.002878332 |
0.996404992 |
1.000368954 |
1.00118953 |
0.999901559 |
0.999455167 |
|
0.984001156 |
1.010765746 |
1.002803945 |
0.996404992 |
1.000368954 |
1.00161958 |
0.999901559 |
0.999455167 |
1.00032179 |
|
1.010765746 |
1.002803945 |
0.993276408 |
1.000368954 |
1.00161958 |
0.99900711 |
0.999455167 |
1.00032179 |
1.000111722 |
|
1.002803945 |
0.993276408 |
1.0019865 |
1.00161958 |
0.99900711 |
0.999688458 |
1.00032179 |
1.000111722 |
0.999783302 |
|
0.993276408 |
1.0019865 |
1.002393272 |
0.99900711 |
0.999688458 |
1.000652758 |
1.000111722 |
0.999783302 |
1.000052518 |
|
1.0019865 |
1.002393272 |
0.99781494 |
0.999688458 |
1.000652758 |
0.999829654 |
0.999783302 |
1.000052518 |
1.000082115 |
|
1.002393272 |
0.99781494 |
0.999901144 |
1.000652758 |
0.999829654 |
0.999759022 |
1.000052518 |
1.000082115 |
0.999932688 |
|
0.99781494 |
0.999901144 |
1.001144355 |
0.999829654 |
0.999759022 |
1.000205706 |
1.000082115 |
0.999932688 |
0.999992604 |
|
0.999901144 |
1.001144355 |
0.999477909 |
0.999759022 |
1.000205706 |
1.000017686 |
0.999932688 |
0.999992604 |
1.000037356 |
|
1.001144355 |
0.999477909 |
0.999689658 |
1.000205706 |
1.000017686 |
0.999888325 |
0.999992604 |
1.000037356 |
0.999985021 |
|
0.999477909 |
0.999689658 |
1.000416401 |
1.000017686 |
0.999888325 |
1.000047001 |
1.000037356 |
0.999985021 |
0.999988812 |
|
0.999689658 |
1.000416401 |
0.999947105 |
0.999888325 |
1.000047001 |
1.000032344 |
0.999985021 |
0.999988812 |
1.000013084 |
|
1.000416401 |
0.999947105 |
0.999818335 |
1.000047001 |
1.000032344 |
0.999960329 |
0.999988812 |
1.000013084 |
0.999999052 |
|
0.999947105 |
0.999818335 |
1.000117298 |
1.000032344 |
0.999960329 |
1.000003665 |
1.000013084 |
0.999999052 |
0.999993932 |
|
0.999818335 |
1.000117298 |
1.000032207 |
0.999960329 |
1.000003665 |
1.000018004 |
0.999999052 |
0.999993932 |
1.000003508 |
It appears that these sequences converge to 1.
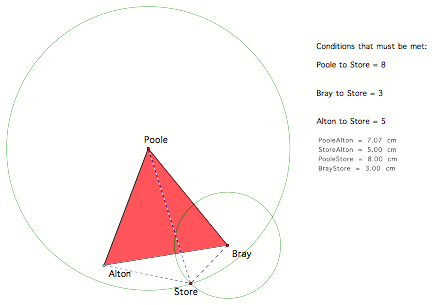
Third Investigation: Where is the Store?
Problem: Three towns in Ireland,
Poole, Bray, and Alton, are located 8, 3, and 5 miles, respectively, from a
store. How far apart are the towns from one another if they are located at the
vertices of an equilateral triangle?
Solution Path and Commentary:
We used the GeometerÕs Sketchpad software program to help us find a solution to
this problem. One of the script
tools is the creation of an equilateral triangle if the user only constructs
one side of the triangle. I then drew an equilateral triangle using this script
tool. I labeled each of the
vertices with the names of the three towns. I then created the point that would
represent the location of the store, and labeled the point as such. Connecting each of the points that
represent the cities to the point that represents the store creates three
segments. The GeometerÕs Sketchpad
program does include the ability to measure the lengths of these three
segments. While measurement may
not be a key concept to classical geometry, it does help us in this particular
problem. If the student can see
that the distance between the store and the city satisfies the given
conditions, then the student would be content with the solution that he or she
has arrived at. Should the
students desire a more rigorous verification of his or her solution, the
student could try an approach that does not require measurement so heavily.
After the distances were first measured, the first goal was to satisfy one of the conditions. Using these measurements, I made the assumption that while the sketch is measured in centimeters, what works for centimeters will work for miles as well. There is a certain amount of guess-and-check work that must be done using this method; however, with the measurements visible in the sketch, we can very quickly see if one of the conditions will be met. As I was completing this problem, I was able to place a point that was 3 miles from the city of Bray. Once that condition was satisfied, I wanted to make sure that any point I selected was 3 miles from that city. In order to keep that distance maintained, I created a circle where the point representing the city is the center of the circle and the point I guessed is a point on the circle. I then selected a point on the circle and tried to find another point that would satisfy one of the two remaining conditions. After more guess-and-check work, I found another point that was 8 miles away from the city of Poole. I also created another circle with the center being a city and a point being the conjectured location of the store. At this point, there were two intersection points for the two circles. I measured the distances between the location of the store to see if either of the intersections would be 5 miles from the third city. When it was not the case, then more guess-and-check work took place. Unlike the previous two guess-and-check methods, not only did I move the location of the store but the length of the triangle that connects the three cities. Once I moved the length of the triangle and the placement of the store, I found a location that did satisfy all three conditions. Once the three conditions were met, I measured the length of the side of the triangle, and determined that for the three conditions to be met, the length of the side of the triangle is 7.07 miles, rounded to the nearest hundredth. I would conjecture that the length of the side is 10 times the square root of 2, based upon the decimal approximation that I received. The GSP sketch below shows the equilateral triangle I used, the segments that connected the cities to the store, and the two circles I used to keep the store 3 miles and 8 miles away from Bray and Poole respectively.