

This assignment called for the investigation of second degree equations. I chose to investigate how changing the values of a, b, and c would change the shape of the graph of the parabola. I decided on this problem because I found it extremely relevant to the Algebra II class I was teaching at the time. We were introducing quadratic graphs and was actually looking for a way to show the students how changing the different values of a, b, and c would change the shape of the graph.
I began by changing the values of A:
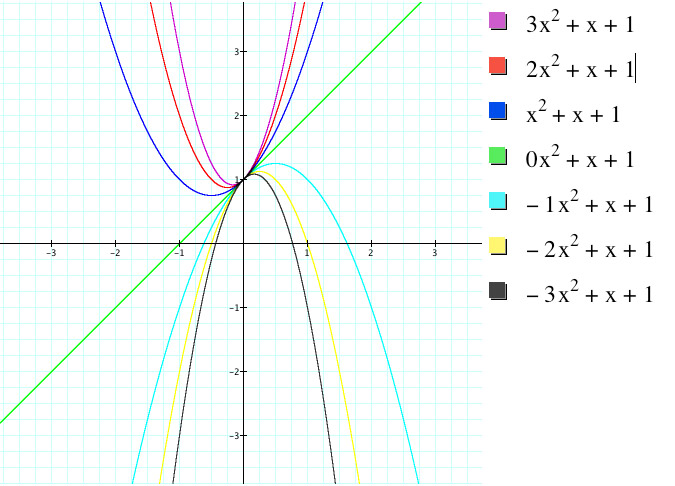
graphing calculator file
The first thing I noticed upon further examination is that all 7 graphs produced shared a single point, (0,1). This is of course because the C term is unchanging and nonzero, so when x=0, the only remaining term of the equation is the C term, which here is 1. Therefore, whenever x=0, y=C for all graphs in this case.
Next, it can be observed that as the value of A increase from 0 to 3, and decreases from 0 to -3, each subsequent graph is contained within the previous graph. This goes with the observation that as the magnitude of A increases, the corresponding parabola becomes narrower.
Lastly we can see that the vertex of each graph is slightly different. This can be attributed also to the changing value of A in each equation. We know that the x-coordinate of the vertex of a parabola is located at x = -b/2a. Therefore as the value of A increases, the vertex will shift to the left until a=0 and as the value of A decreases, the vertex will shift to the right until a=0. We can see that when -1 < a < 1 the vertex moves rapidly out until a = 0 and the vertex is not-existance as witnessed by a linear function, y= x+1.
Next I fixed the values of A and C, and changed the values of B:
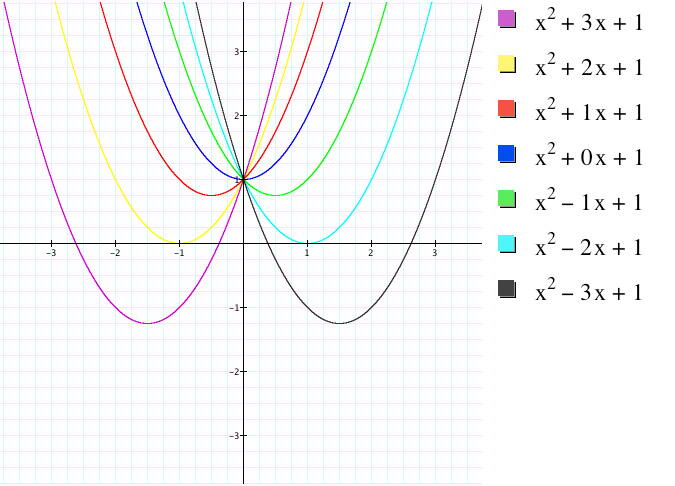
graphing calculator file
We can see that no matter what the value of B is, the narrow-ness of the parabola will remain the same. This adds further evidence to our previous claim that it is the value of A that changes the narrowness of a parabola. We can also see that if we change the value of B, all the parabolas will share the same point from when we varied A, (0,1). Again we can figure this out because all the C values are non-zero so when x=0, y= C.
We can see that the x-coordinate of the vertex is also affected by the B value of an equation. Again, we know that the x-coordinate of a vertex is given by -b/2a. In this case, A=1 so the vertex is given by -b/2. The most interesting characteristic of this set of graphs is that if we were to draw a curve through all of the vertices, the curve would be a parabola. This makes sense because to determine the y-value of a vertex, we simply plug the x-coordinate of the vertex in the orignial equation, which is a quadratic. Therefore our outputs should also follow a quadratic pattern.
The last case I examined was when A and B were fixed and C was varied:
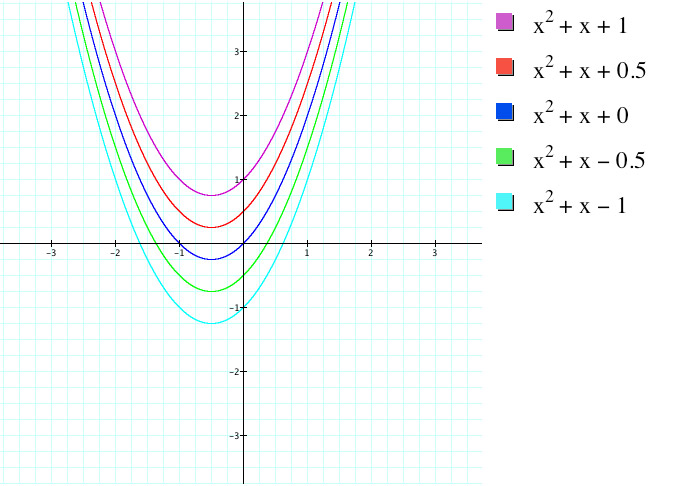
graphing calculator file
What is interesting here is that we can see that none of these parabolas share a point(s). Our previous assertations that A determines how narrow a parabola is can be given further evidence as all of these curves have the same A value and are equally narrow. In addition our previous conjecture that a combination of A and B determines the x-coordinate of the vertex of a parabola can also be seen in this case. When only the C value varies, the x-coordinate of the vertex of every parabola is the same (assuming the A and B values are the same)
Lastly, I was interested to see how these parabolas would look relative to each other at all values. To do so, I animated the parabolas on a graph together. In the purple curve, the A value is varying, the red curve the B value, and the blue curve, the C value. Values varied from -3 to 3.
graphing calculator file
We can see now how all these varying values related to each other. The most interesting case is when all three parabolas are identical. This is when all three equations for the parabolas equal x^2 + x + 1. An extension to this investigation that may be interesting would be to look into if there is always a case that where all 3 parabolas will be identical.