

For assignment #3 I have chosen to investigate x^2 +bx + c = 0 in the xb plane. To begin I plotted the graph with values of a = b = c = 1. This should give us some reference graph to compare to when we change the values.
Next I wanted to see how this might look in 3 dimensions, so again I plotted the original equation into the xyz-plane:
The investigation calls for us to analyze this graph with the graph of b=3. If the two graphs intersect, we know that the intersection points correspond to the roots of the original equation. What I was interested in finding is for what values of C returned roots. To begin investigating this I graphed the line b=3 and several graphs with varying C values:
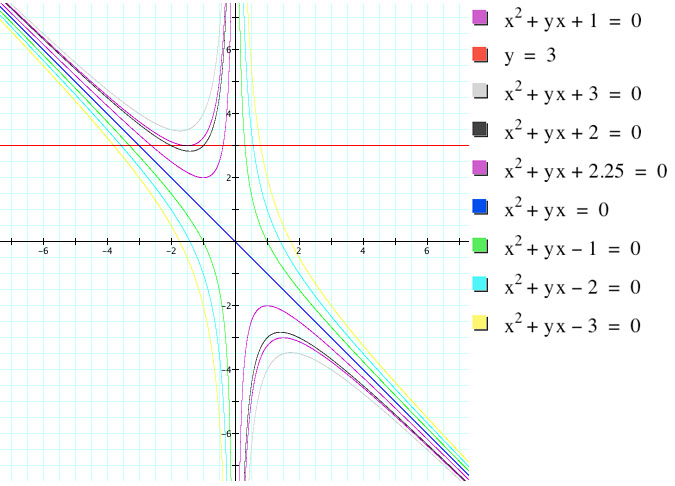
Next, I let C = n in Graphing Calculator so I could see how the graph would change with different values of n over time, so I animated the graph x^2+yx+n=0 from n= -10 to +10, 200 steps:
By viewing this animation we can see all the different cases of this graph and its roots. When c < 2.25 there are no real roots, when c = 2.25 there is one real root, when 0 < c < 2.25 there are two positive real roots, and when c < 0 there are 2 real roots, one positive and one negative. What becomes interesting now is finding what c must equal for the given equation to have only 1 real solution when given a y value.
I began by trial and error. I would enter a value for the equation y = # and then find the c-value that would could the curve to only touch the line once. I computed c-values when y = 1, 2, ..., 9. I then performed several regressions on the data and found that a power regression would fit the data perfectly. From this regression, I found that the c-value must equal .25*y^2 for a given y value. The animation below is the graph of x^2 + xy + .25n^2 = 0 (purple) and y = n (red):
We can see that y=n is always at the minimum/maximum of the curve. We can safely say that given a value we want the minimum or maximum of a equation in the form x^2 + xy + c = 0 to be at, we must substitute .25n^2 in for c and we are done!
We can confirm this by using the fact that the x-coordinate of the vertex is -b/2a, which is xy/2 in this problem. To help simplify this expression, we can use the caluculus fact that the derivitive of an equation results in its slope, and the value of the derivitive when equal to 0 is a vertex. This expressions derivitive is 2x + y = 0 which implies x=-y/2. Plugging this back into our original idea of using xy/2, we get -y^2/4 for our needed value of C. This checks out because both positive and negative y^2/4 will result in either a maximum or minimum.