
Class Page for Taylor Gibson
Assignment 7: Loci of Tangent Circles
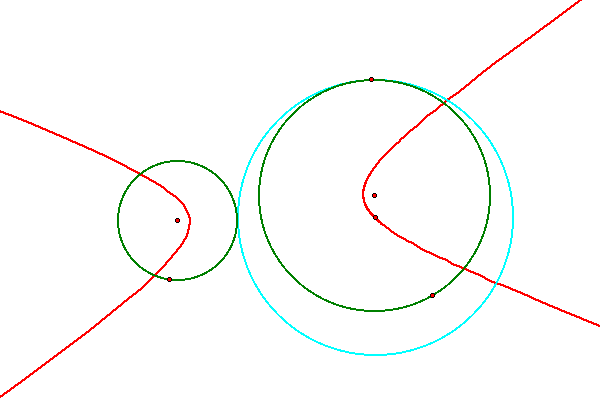
For assignment #7 I have chosen to investigate the loci of tangent circles. I followed the construction methods found on the assignment #7 webpage to construct two sets of tangent circles. Each set of circles consists of two given circles, and a point on one circle. From this information we can construct a circle tangent to both circles on the outside, and a circle tangent to the two circles on the inside. Below is the JavaSketchPad of the circle constructed (blue) to be tangent to two given circles (green) on the outside. The locus of the center of the constructed tangent circle is marked in red:
After playing around with this construction we can find several interesting observations about the locus of the center of the tangent circle. The locus will always result in a conic section with the foci being the centers of the original two circles. In addition the locus will also always pass through the center of the constructed tangent circle. There will be three distinct cases of conics: an elipse, a circle, and a hyperbola:
When one circle is inside the other, the locus takes the shape of an elipse. We can see from the construction that the sum of the distances from the centers of the two given circles is a constant. It follows that the constant distance will always pass through the center of the tangent circle.:
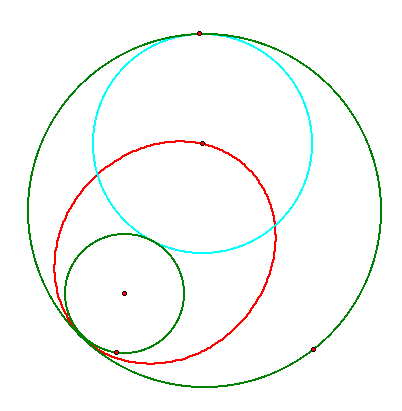
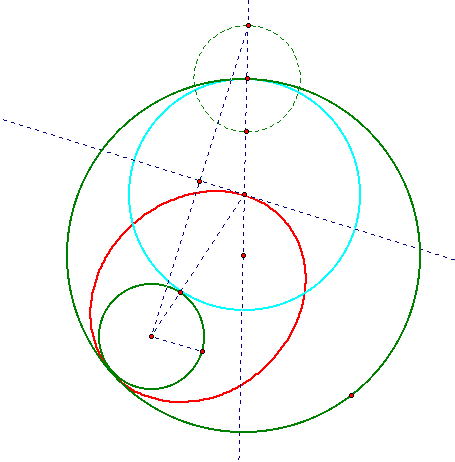
When one circle is intersects the other, the locus takes the shape of an elipse, and the elipse will intersect at the intersection of the two given circles. This can be proven to be an elipse in the same way as above:
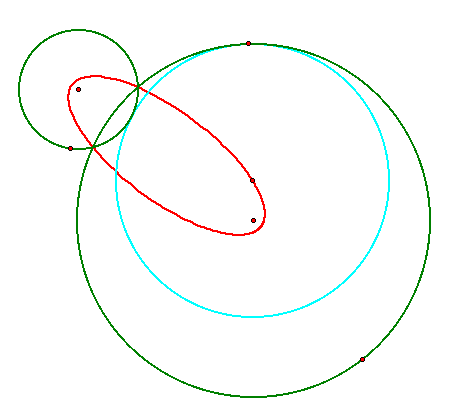
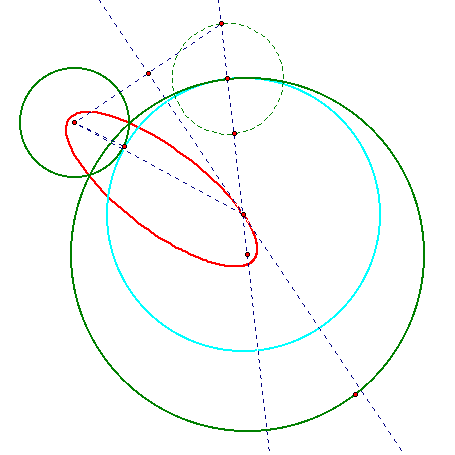
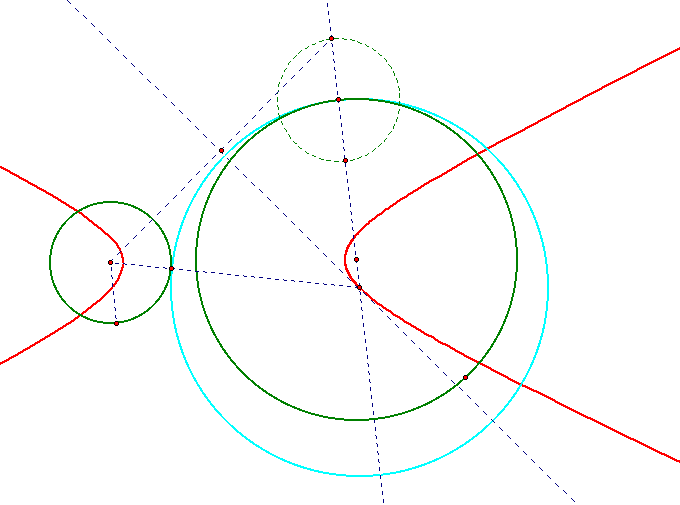
When the two circles are disjoint, the locus takes the shape of a hyperbola. We can see from the construction that if the difference of the distances from the centers is constant it gives us the hyperbolic locus:
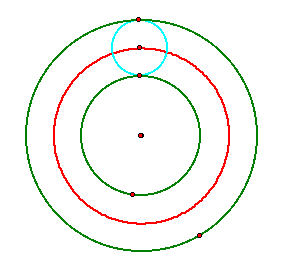
When one circle is concentric with the other, the locus takes the shape of another circle with the same center as the two given circles. We already know the locus will be an elipse, but in this special case the two foci are the same, thus creating a circle:
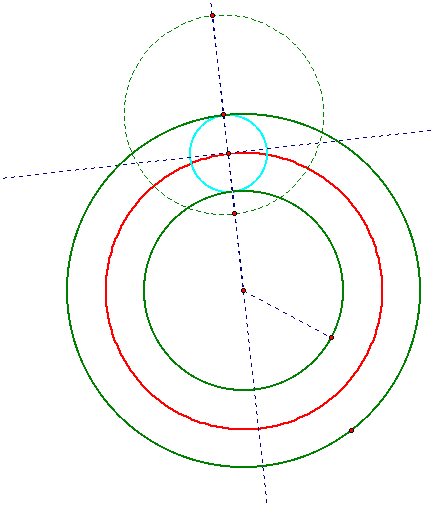
Now, let us investigate the cases where the circle constructed is tangent on the interior of the circle. Below is a JavaSketchPad of the construction with which one can illustrate all the given cases:
Again, after some investigation several interesting trends can be found in this construction. Once more we will find several conic sections emerage as the locus of the center of the constructed tangent circle. Because the construction is so similar to those found above, the proofs of the shape of the loci are pratically the same.
When one circle is inside the other, the locus takes the shape of an elipse:
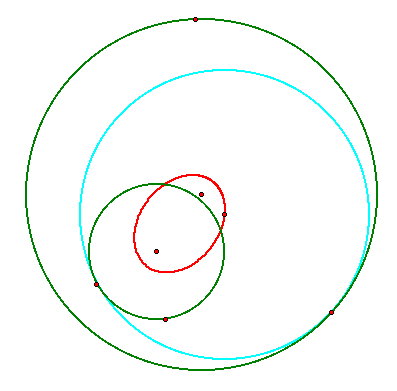
When one circle is concentric with the other, the locus takes the shape of another circle with the same center as the two given circles:
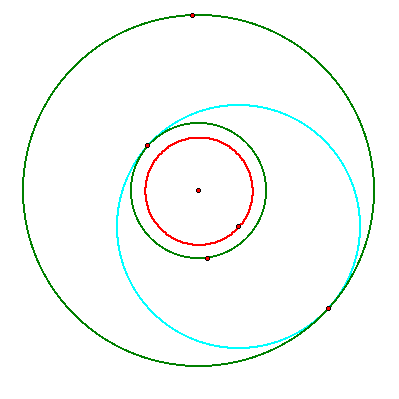
When the two circles intersect, the locus takes the shape of a half-hyperbola that also intersects at the intersection of the two given circles:
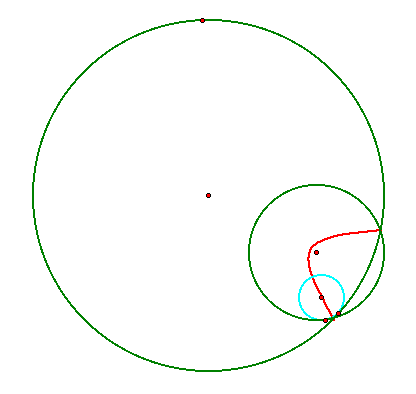
Return to Taylor Gibson's 6680 Page












