

Our good friend Barney has found himself trapped in a very large and very dark triangular room (which happens to the best of us from time to time). He'd like to explore the room but is afraid that he'd get lost forever. Remembering a particular geometry problem he learned in school, he decided to head off until he hit a wall and then walk parallel to the wall he just left, knowing well that eventually he'll come back to his original location. Is Barney crazy, or does his idea actually make sense? Let's investigate his claim.
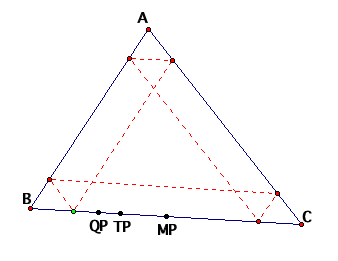
We can find some interesting things about Barneys plans if we take the time to analyze his path. Lets see what would happen if he started at the trisection of the wall he's on.
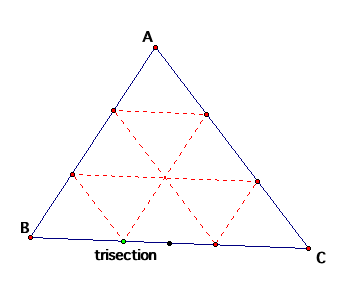
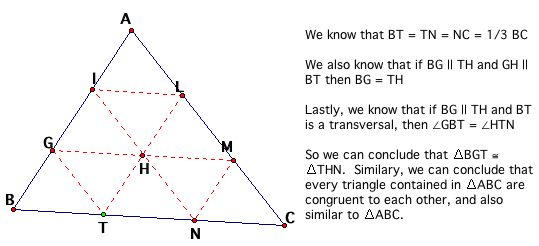
We see that it appears that Barney will cross over the same point 3 times on his trek around the room. In fact, if we look at his path, he has divided the room into 9 congruent triangles! Let us see if this is true:
Now let's take a look to see what would happen if he were to leave from the midpoint of the wall he's on.
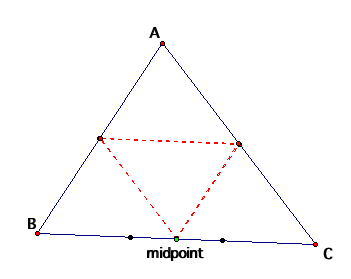
Looking at his path we can see that he'd only have to go around the room once to get back where he started. It would also appear that his path would divide the room into 4 congruent triangles. Here is the proof:
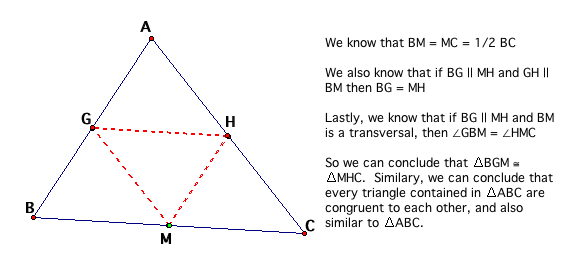
Lets now look at what whould happen if our friend Barney started at the quadsection point of the wall he's on.
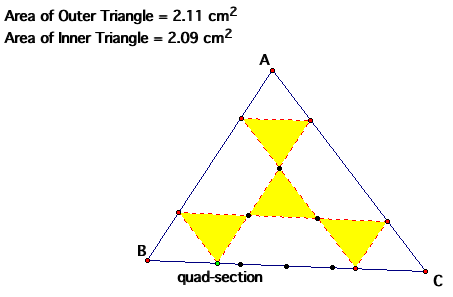
Using the same logic and proofs found above, we can prove the 4 yellow triangles to be equal, and thus have the same area enclosed in them. It becomes hard to verify this in GSP due to pixel problems, but we can get a pretty close measurement.
Let's now take a look at what if Barney should start in a corner of the room. It should be fairly obvious that this would lead to Barney getting back to where he started, and we can see this with our diagram:
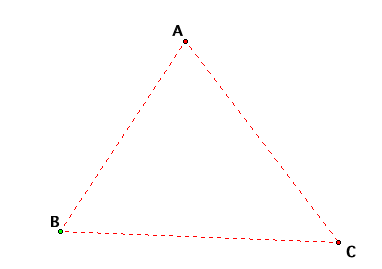
Another intresting observation about Barneys route is that no matter where he starts from, he will always walk the same distance to get back to where he started, and this distance is equal to the perimeter of the triangular room. See for yourself in the JSP below:
Lastly, let's take a look at a case that is not physically possible for our situation, but we'll look at it anyways. What if Barney were actually outside of the room, and would change direction if he were to hit a theorhetical extension of the wall. Let's take a look:
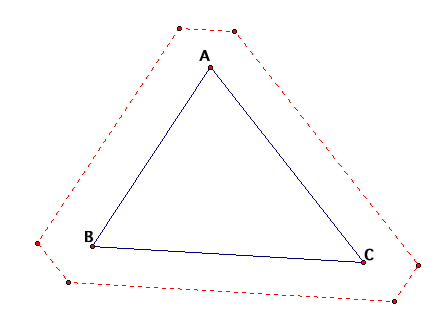
Even in this "impossible" case, our good friend Barney would still find his way back to where he began.
[GSP SKETCH]