The Golden Ratio in Architecture

By:   Christa Nathe & Kate Hobgood

 

Proportions and the Golden Ratio

In order to better understand the Golden Ratio, it is helpful to have an understanding of the mathematical term proportion.  The Columbia Encyclopedia defines the term proportion in mathematics as the equality of two ratios.  Two pairs of quantities a, b and c, d are in proportion if their ratios  and  are equal  In other words, the two pairs of quantities are in proportion if the equation  holds true.  When considering the Golden Ratio, the quantities refer to lengths of line segments. 

In these terms, the Gold Ratio is a division of a line segment into two segments that such that the ratio of the original segment to the larger division is equal to the ratio of the larger division to the smaller division.  Let C represent the original segment, A the larger division, and B the smaller division.  It is helpful to picture the line segment as follows:

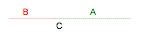
It follows that C = A + B and.  Therefore, A is the geometric mean of B and C, and is commonly referred to as the Golden Ratio.

The Golden Ratio is also referred to as the Golden Rectangle, the Golden Section, the Divine Proportion, and Phi ().  Phi is defined as an irrational number that has unique properties in mathematics in which  is the solution to a quadratic equation.  Phi is the ratio  and the three properties are as follows:

     

       (No other number has this characteristic)

       (Phi is the solution to a quadratic equation)

When using the last property, we can find the value for  by using the quadratic equation.  There are two solutions to this equation is and 0.618033988749894848.  Given these two values, we define upper case Phi or = 1.618 and lower case phi = 0.618.

Referring back to the length of the line segment, C is 1.1618 times the length A, and A is 1.1618 times the length of B.  Alternatively, B is 0.618 of A, and A is 0.618 of C.  The Golden Ratio most commonly considers  as being the positive solution, or = 1.618. 

Construction of Golden Rectangle using GSP

The Golden Ratio and Phi have been used in various geometrical constructions throughout history.  This distinctive ratio can be found in the human body, nature, solar systems, DNA, the stock market, the Bible and theology, music, artwork and design, and architecture.  Even though the Golden Ratio is found in several aspects of culture and science, one can experience the ratio visibly in structures of ancient and modern architecture.

The Golden Ratio and Ancient Greek Architecture

         The Greeks were aware of the pleasing aesthetics effects of the golden ratio.  Appearing in many architectural structures, the presence of the golden ratio provided a sense of balance and equilibrium.  The geometrical figure of the golden ratio is essentially pleasing and easy on the eye. 

For instance, consider the Greeks ancient Parthenon located in the Akropolis in Athens, Greece.  The Parthenon was built in the 5th century B.C. when the Athenian Empire was influential and models the power and supremacy of the empire.  It was dedicated to the Greek goddess Athena.  The temple was constructed by three architects during Iktinus, Callicrates, and Phidias.  The symbol for the golden ratio, the Greek letter phi-, was named after the sculptor Phidias.  The golden ratio appears in several constructions and layouts of the Parthenon. 

Beginning with the exterior of the building, the dimensions of the faade represent the perfect golden ratio.  The aligning of the rectangular front of the temple can be seen in the figure below:

Image from www.goldennumber.net

 

The following diagram may provide a more clear representation of the golden ratio in the faade of the Parthenon:

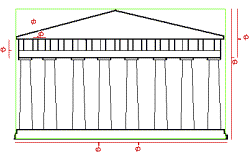
In the above figure, one can see the use of a golden rectangle that is Phi times as wide as the height of the structure.

Notice the rectangles constructed and the highlighted portions of the segments.  Each segment length of the rectangle follows the golden ratio, where the ratio of the lengths of the smaller yellow segment to the larger blue segment is equal to the ratio of the lengths of the blue segment to the whole white segment.

The golden ratio can also be found throughout the floor plan of the Parthenon:

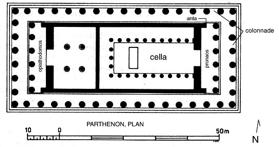
The floor plan area is a  rectangle:  the length is  times as long as the width of the ancient temple.  Despite the numerous mathematical occurrence of the golden ratio in the construction of the Parthenon, there are no historical records of the original plan of the temple.

Proof of the Golden Ratio in the Parthenon GSP sketch

 

The Golden Ratio and the Great Pyramids

 

Image from Culturefocus.com

 

         The most famous monuments of ancient Egypt are the Great Pyramids of Giza.  Believed to have been constructed around 4,600 years ago, these pyramids were built around the golden ratio, long before the Greeks and the Parthenon.  The largest of the pyramids in Giza contains the use of phi and the golden ratio.  The golden ratio is represented as the ratio of the length/height of the triangular face to half the length of the square base. 


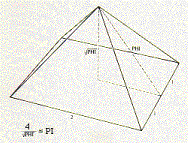
Image from Valdosta Museum website.

      The length of the base of the pyramid is approximately. 

      The height of an isosceles triangular face is approximately phi.

       The height of the pyramid is approximately the square root of phi.

      The height can then be found as .

      The slope of the pyramid is very close to the golden pyramid inclination of 51 50.

Note that the values used in these ratios are approximate.  Due to the age of the architecture, much of the material has eroded, been extracted, or altered due to natural means.

The Golden Ratio and Notre Dame

Image from Wikipedia

 

         Phi and the use of the golden ratio are found in the design of Notre Dame in Paris, France.  The Gothic Cathedral was built beginning in the year 1163, and completed in the year 1345.  Claimed as the first Christian church in Paris, Notre Name was built upon the Roman temple of Jupiter.  The west faade of the church was completed around the year 1200, and it is here where the presence of the use of the golden ratios is visible.  See the image below with the highlighted segments emphasizing the ratio.

Image from GoldenNumber.net

 

The Golden Ratio and the UN Building

Image from library.thinkquest.org

The current headquarters for the United Nations was constructed on an 18-acre piece of land in the East side of Manhattan. Following World War II, the United Nations was established to help intervene in future global conflicts, such as aggression, that would in hope avoid another world war. The organization was established and the headquarters were built under the supervision of lead architect, Wallace K. Harrison from the United States. Although Harrison is not typically known to use the golden ratio in his designs, a French architect Charles E. Jeanneret was on a team of assisting architects. Charles E. Jeanneret was known to frequently use the golden ratio in his architectural designs. When constructing the United Nations headquarters, the team of architects decided to use this ratio in a couple of different ways. When looking closely at the building we observe that many of the windows in fact have the golden ratio when comparing their width and height. The more obvious application of the United Nations headquarters to the golden ratio is found when looking at the width of the entire building and comparing it to the height of every ten floors.

The Golden Ratio and the CN Tower

 

 

         The unique ratio that the Golden Ratio and Phi represent is undeniably a remarkable concept of mathematics.  The presence of the Golden Ratio has been found in architecture dating over 4,000 years ago.  From the ancient Great Pyramids to the modern CN Tower, the aesthetically pleasing aspects of is ever present. 

Association to the Fibonacci Sequence

Let f1, f2 , f3 , , fn denote the values of the Fibonacci sequence. Observe that each number of the sequence is the sum of the two numbers before it. For example, 1 + 1 = 2 or using our notation, f1 + f2 = f3. One can verify this method using the left column of the spreadsheet below.  Interestingly enough, the Fibonacci sequence has a surprising relation to the golden ratio. If one divides f6 by f5, the value is almost phi. The higher the number in the sequence, the closer the ratio is to phi. Notice from the right column of the spreadsheet  that the approximation of phi jumps around.  However, as the values of the ratio increase, the approximation begins to gain consistent decimal place values, yielding a better approximation of phi. 

 

1

001/001

1

1

002/001

2

2

003/002

1.5

3

005/003

1.666666667

5

008/005

1.6

8

13/8

1.625

13

21/13

1.615384615

21

34/21

1.619047619

34

55/34

1.617647059

55

89/55

1.618181818

89

144/89

1.617977528

144

233/144

1.618055556

233

377/233

1.618025751

377

610/377

1.618037135

610

987/610

1.618032787

987

1597/987

1.618034448

1597

2584/1597

1.618033813

2584

4181/2584

1.618034056

4181

6765/4181

1.618033963

6765

10946/6765

1.618033999

10946