Assignment 1: Graphs

by

HULYA KILIC

In this assignment, I want to explore the changes in the graph of xⁿ + yⁿ = 1 where n=2,...25. I start with graph of x² + y² = 1 which I know that it is a circle having radius 1 and centered at the origin. Then I tried x³ + y³ = 1. It is a curve passing through the points (1,0) and (0,1). Then I tried x⁴ + y⁴ = 1. It has a shape between a circle and a square. Then I wonder about x⁵ + y⁵ = 1. It was a curve again passing through the points (0,1) and (1,0) but it was passing above the curve of x³ + y³ = 1 between x=0 and x=1, but below the curve for the other values of x. Then I tried x⁶ + y⁶ = 1 and x⁷ + y⁷ = 1. Again I observed that for x⁶ + y⁶ = 1, I get a shape between a square and circle such that much more close to the shape of a square and for x⁷ + y⁷ = 1, I get a curve intersecting with the previous curves at the points (0,1) and (1,0) and lies above the curves between x=0 and x=1 and lies below otherwise.

Here the graphs of those equations.

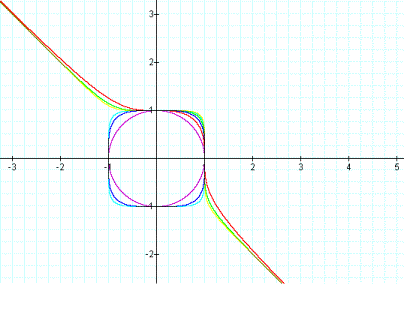
I guess that if I continue in that manner, for even powers of the equation, I will get a shape between circle and square and for the odd powers I will get a curve passing through (0,1) and (1,0) and each curve is above the previous curve between x=0 and x=1, but below the curve for the other values of x. I continued to try the equation upto x²⁵ + y²⁵ = 1. And the picture of what I get is below.

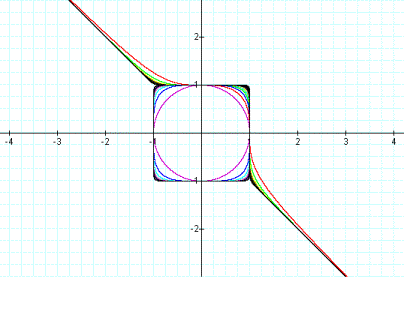
From the picture it seems that the graphs of even powers of the equation and odd powers of the equation converges to each other between the values of x=-1 and x=1 at the right part of the picture.

Then I tried the equations for the higher powers. I observe that graph much more turns out to be a squared shape.

Click here for the animation.

Then I wonder about the other side (left part) of the graph. Whether there exists graph of an equation which converges to the graph of even powers of the equation. So, I decided to start with negative powers of the given equation, i.e. x^-n + y^-n = 1.

First I tried x^-1 + y^-1 = 1. Its graph does not exactly match what I expect. Then I tried x^-2 + y^-2 = 1. It was much more similar to what I expect. Then I tried the graph of x^-3 + y^-3 = 1. Its shape similar to x^-1 + y^-1 = 1. So, I tried x^-4 + y^-4 = 1. Its graph similar to x^-2 + y^-2 = 1. Then, I decided to focus on negative even powers of the equation.

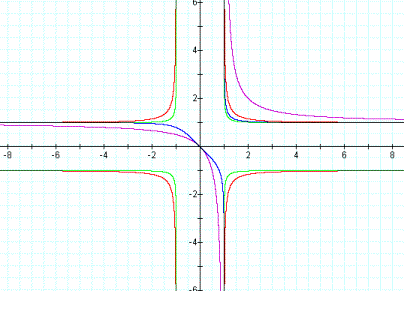
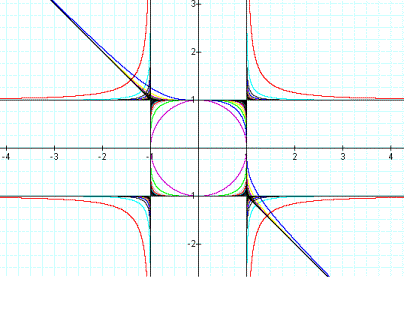
I look at the final graph of the combination of original graphs and the graphs of equations having even negative powers. It is similar to what I expect since new graph touches the original graph at x= -1. But it was not the symmetric of the graphs of the equations having odd powers.

Then I consider to try the graphs of function where n is an odd number greater than 1. Then I get the following graphs for n=3,...9

Still, it was not the symmetric with respec to the origin. Then I changed the places of x and y and look at the graphs of function where n is an odd number greater than 1. Then I get the following graphs for n=3,...9

Then I decided to combine last two functions with the original equation. Here, what I get:

This graph is what I tried to get:)