Gaussian Integers &
Division Algorithm Project
By: Clay Kitchings
MATH 6000
(Also EMAT 6690)
Motivation
for this write-up comes from my MATH 6000 project/assignment on the Gaussian
Integers. This will become a webpage
“essay” for EMAT 6690. This
assignment makes use of the following technologies: TI84 Plus Silver Edition
(for “efficient” multiplication of complex numbers), Geometer’s Sketchpad (for
plotting points and for other graphics). Note: This link will NOT be activated
until after 11:00am, Thursday, May 3rd. No one (teacher, student, or other individual or group)
other than Clay Kitchings will view this document in any shape or form until
after the 11:00am deadline.
A
Gaussian Integer is a complex number a + bi where a and b are both
integers.
Let this
set be represented by Z[i] = {a+bi |
a, b are in Z}.
Like Z
and F[x] (and a few other rings) Z[i] has a division algorithm. Our first goal
is to see how the division algorithm works:
The
Division Algorithm, also known as “Proposition 3.1” states the following: “Let z = a + bi and w = c + di (z, w,
elements of Z[i]), ![]() .
Then there are Gaussian integers q and r so that z = qw + r with |r|2
< |w|2 ” (Shifrin, 1996, p. 140).
.
Then there are Gaussian integers q and r so that z = qw + r with |r|2
< |w|2 ” (Shifrin, 1996, p. 140).
For our
first example, let z = 4 + 7i and w = -1 + 4i.
For the
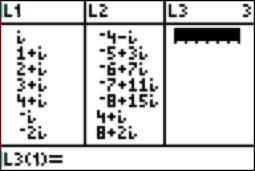
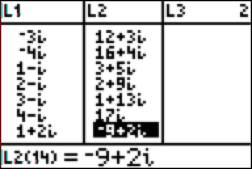
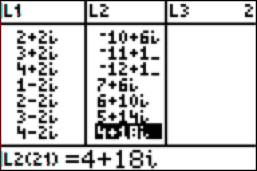
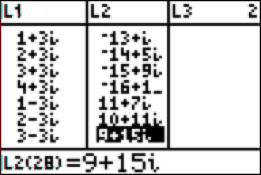
record, we’ll compute some multiples of w. We’ll use the TI84 to expedite the
process. L2 = L1*w:
1) On the following grid, we shall
mark all of the points in <w>, the ideal generated by w. Note that the horizontal axis is the
real axis and the vertical axis is the imaginary axis (though it is only labeled
as a typical x-y plane).
2) We’ll connect some of the points
in <w> and tile the plane with squares. This process was initiated by
drawing the polygon with vertices 0, w, iw, and (1+i)w.
3) Next, we’ll plot z in the complex
plane (as shown below).
4) The yellow-colored point z now
lies in the interior of one of the squares above. Since the vertex is in
<w> it is of the form qw for some q in Z[i]. The vertex of the square nearest to z is (1-i), so q = 1-i.
5) Now let r = z – qw. What is
r?
![]()
6) Claim: We have just applied the division
algorithm to z and w.
Discussion: We have applied the division algorithm because
we’ve expressed z as a product of w and a Gaussian integer plus some remainder
(also a Gaussian integer). All of the vertices with blue points are in
<w>. The w vertex itself is also highlighted yellow.
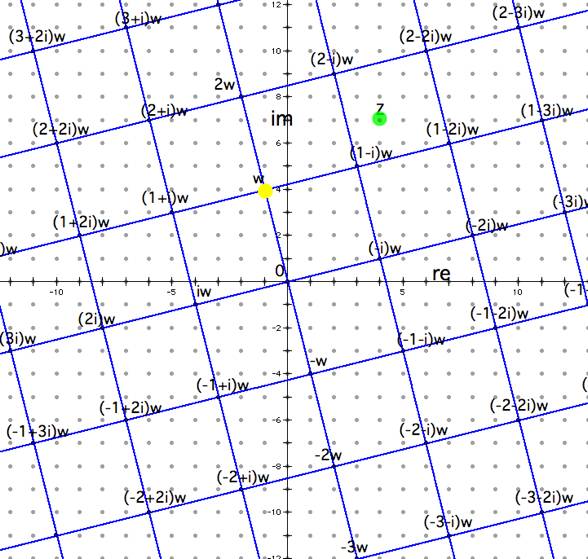
Note
(visual observation): we may observe a pattern along each line passing through
the points in <w>. For
example, after calculating various multiples of w (i.e., various forms of qw),
we find that a pattern exists within the real and imaginary parts of the
complex number q. For example, the points which are collinear with w and (1+i)w
all have 1 as the real part of q. We’ll call that line L1. The “parallel” line immediately below
L1 has 0 for all the real parts of each complex number q. Immediately below and
“parallel” to that line, we find a similar result for the real parts of q,
except for now it is -1. As we proceed downward in the plane, we find that for
each line the real part of the number q decreases by one.
There is
a similar pattern that occurs for those lines which are perpendicular to
L1. As one moves further to the
left in the plane, one finds the imaginary part of the number q increases by
one (or rather, the coefficient of i increases by one for the complex number
q). Moving to the right causes the coefficient of i to decrease by one with
each additional line to the right in the plane. This pattern is useful in more
quickly determining the vertices of the squares (all of which are in <w>).
Now
repeat the steps above with z = -1 + 4i and w = 1 + 2i. Why are we using these
numbers? They come from the above problem’s continuation of the division
algorithm.
From
above, we have the following:
r = z – qw However,
if we are to continue to “divide,” we would then repeat the process as follows:
z = w – q’w’ for
some new q’, w’ that are in Z[i].
This process is somewhat analogous to finding the gcd(14, 35) among the
integers by using the Euclidean Algorithm.
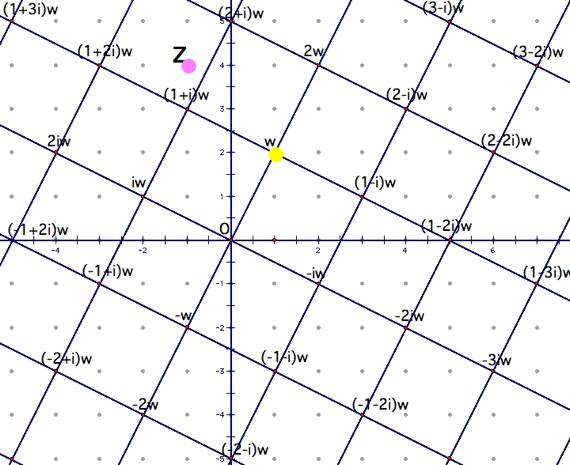
The above
graphic illustrates the complex number w along with the ideal generated by w
(or <w>). The pink-colored point z lies in the interior of one of the
squares, and it is closest to the vertex (1+i)w. This vertex is a part of
<w>, so it is of the form qw for some q in Z[i]. This means q=1+i.
Let r = z
– qw, and solve for r: r=
(-1+4i) – (1+i)(1+2i) Ź r=
i = (0 + 1i)
Calculate
gcd(4+7i, -1+4i).
z = (q) (w) +
r
4+7i =
(-1+4i)(1-i) + (1+2i)
-1+4i =
(1+2i)(1+i) + i
1+2i =
i(-i+2) + 0
So,
gcd(4+7i, -1+4i) = i.
Now,
write the gcd as a linear combination of (4+7i) and (-1+4i). Let these two complex numbers be z and
w as they were earlier in the problem.
So now we need to write i as a linear combination of z and w.
i = w
– (1+2i)(1+i)
i = w
– [z – w(1-i)] [1+i] = w – [z(1+i) – w(1-i)(1+i)] = w
– z(1+i) + w(2) = 3w – z(1+i)
So i =
(3+0i)(-1+4i) + (4+7i)(-1-i)
Next, we
shall find the gcd (7-4i, 1+3i).
7-4i =
(1+3i)( q ) + r
Use a
diagram/grid:
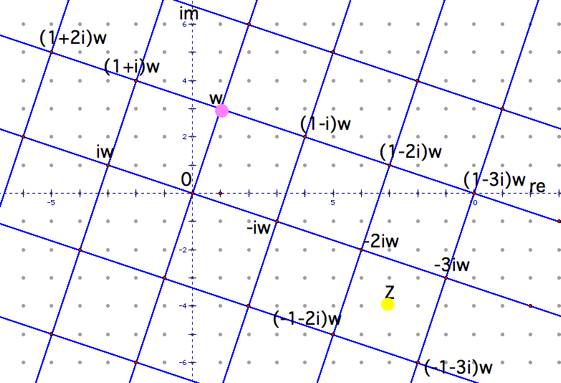
Note: z may
not have one unique “nearest” vertex, so this number need not be unique.
Take q =
-3i.
7-4i =
(1+3i)( q ) + r
7-4i =
(1+3i)(-3i) + r Ź r = -2-i.
So,
7-4i =
(1+3i)(-3i) + (-2-i)
Now we
consider “dividing” (1+3i) and (-2-i):
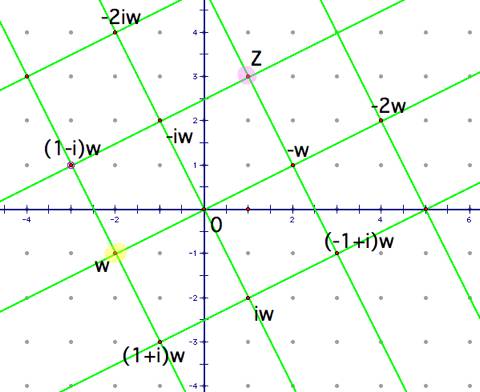
It appears
Z may actually be one of the vertices of a square in the ideal this time.
(Note: this z and w are different from the one’s we started with.) The vertex
“nearest” z is (-1-i)w, so q=(-1-i). Let’s now divide again:
7-4i =
(1+3i)(-3i) + (-2-i)
1+3i =
(-2-i)(-1-i) + r’ where
r’ is some new remainder
Ź r = 0
Therefore,
the gcd(7-4i, 1+3i)
= -2-i. Now we shall write it as a linear combination of z and w:
-2-i = z
– (-3i)(1+3i) Ź -2-i
= (7-4i) + (3i)(1+3i)
References
Shifrin,
Theodore. (1996). Abstract algebra: A geometric approach. Upper Saddle River, NJ. Prentice
Hall.