Write Up #3 :: Parabolic Transformations and a Locus of Points
Clay Kitchings

Consider the parabolas formed by f(x) = x² + bx + 1, where b = -3…3.

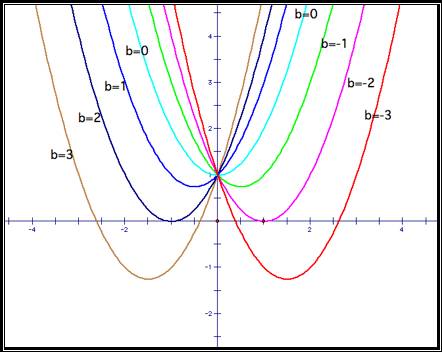
After some observations of what happens as the b-values change, one may see a pattern forming with the vertices of each of the parabolas in the image above. The image below illustrates the potential pattern with the dashed line (curve):

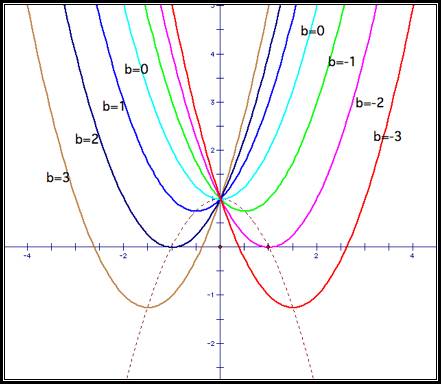
Conjecture: The dashed line is itself a parabola that passes through the vertices of each of the original parabolas. How could we show that this is indeed the case?

Consider the vertices of each of the original f(x) functions. We could find these using a variety of methods. I used the derivative of f(x) to find the minimum x-value, and from there I found the corresponding y-value. The table below contains each of the functions and their corresponding vertices:

f(x):	x-value-vertex	y-value-vertex	Vertex:
x^2-3x+1	1.50	-1.25	(1.5, 7.75)
x^2-2x+1	1.00	0.00	(1, 0)
x^2-x+1	0.50	0.75	(0.5, 1.75)
x^2+1	0.00	1.00	(0, 1)
x^2+1x+1	-0.50	0.75	(-0.5, 0.75)
x^2+2x+1	-1.00	0.00	(-1, 0)
x^2+3x+1	-1.50	-1.25	(-1.5, -1.25)

One test for whether or not a function is quadratic is to determine “finite differences.” If the second-order differences are constant, then the function is quadratic.

f(x):	y-value-vertex	1st differences	2nd differences
x^2-3x+1	-1.25
x^2-2x+1	0.00	-1.25
x^2-x+1	0.75	-0.75	-0.50
x^2+1	1.00	-0.25	-0.50
x^2+1x+1	0.75	0.25	-0.50
x^2+2x+1	0.00	0.75	-0.50
x^2+3x+1	-1.25	1.25	-0.50

An evaluation of the differences in y-values shows a pattern of constant differences at the second level. This implies that the dashed curve above is quadratic, and therefore a parabola. Now, how do we determine a specific equation for this parabola?

Any three points determine a parabola. (Why?) We also assume these three points are noncollinear as that is a trivial case (a degenerate parabola or a line). Any three of the vertices above are noncollinear, so we may proceed to find this equation.

I will choose the three vertices with somewhat “nice” numbers. I will choose the vertices (1, 0) (0, 1) and (-1, 0).

We can generate equations using each of the points mentioned in the last sentence from the equation of a parabola in standard form: f(x) = ax² + bx + c. We will substitute values of x and y into the function to generate three distinct equations:

Vertex (1, 0): f(1) = 0 = a + b + c è a + b + c = 0

Vertex (0, 1): f(0) = 1 = c è c = 1

Vertex (-1, 0): f(-1) = 0 = a – b + c è a – b + c = 0

Notice that we now have three equations with three unknowns. Therefore we can solve a system of equations by any appropriate preferred method. I will use a 3x4 augmented matrix and row reduce it to find the values of a, b, and c. The reduced row-echelon form of the augmented matrix is:

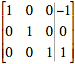
Therefore, a = -1, b = 0, and c = 1. Furthermore, if we substitute these values in for f(x) = ax² + bx + c, we obtain the equation:

f(x) = -x² + 1