EMAT 6680 Write Up # 4a :: Clay Kitchings :: How To Construct a Specific Triangle Given the Medial Triangle

I recently made an observation concerning the Medial Triangle and its relationship compared to its “parent” triangle. So what if the typical question were asked in reverse? Example: “Given the Medial Triangle DEF, find the three points of the original Triangle ABC.”

I was recently considering the Triangle Midsegment Theorem (for a proof of said theorem). As I constructed the triangle with GSP, I decided to hide certain portions of the segments of the triangle. As I began to hide various segments of Triangle ABC, I came across this picture:

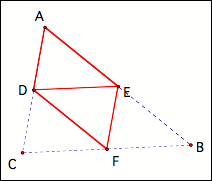
I saw that there seems to be a parallelogram formed (ADFE). Based on the Triangle Midsegment Theorem, we do indeed have a parallelogram if D, E, and F are the midpoints of the segments of the triangle ABC. Then I thought, “If I have a triangle, I have the ability to construct a parallelogram. If I can consider the Medial Triangle problem in this light, I can construct a triangle given the Medial Triangle of that original triangle.”

Prior Supposition: The Medial Triangle creates three parallelograms, each whose opposite vertices are: 1) midpoints of triangle ABC, and 2) a midpoint on a segment and the vertex opposite that side. Reference the figure above. Is ADFE a parallelogram? According to the Triangle Midsegment Theorem, we can conclude that EF = AD and AE = DF. Since the opposite sides of this quadrilateral are congruent, it is sufficient to argue that ADFE is indeed a parallelogram.

Let us construct a triangle ABC given the Medial Triangle DEF of that triangle… shall we?

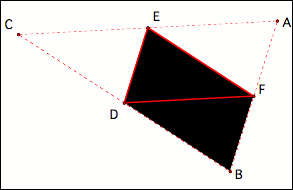
Let’s start with triangle DEF, and we’ll assume that these form the Medial Triangle of the “mystery” triangle ABC. How can we find the points A, B, and C such that triangle DEF is the Medial Triangle? The Medial Triangle DEF is given below. (Note the appropriate colors: Red and Black, the color of champions! – that’s an exclamation point, not meant to be a factorial.)

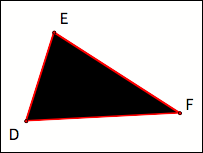
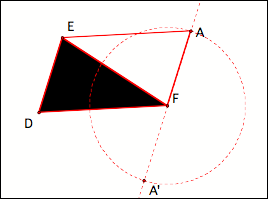
Let us construct a parallelogram DFAE. (Note: one could argue similarly for a point A’ which would create another parallelogram DA’FE “below” segment DF in the figure.) This will not change the argument here.

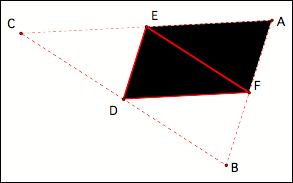
Basically we are going to construct other parallelograms in order to find points B and C of our “parent” triangle. The parallelograms (CEFD, EFBD, and DFAE) are illustrated separately below:

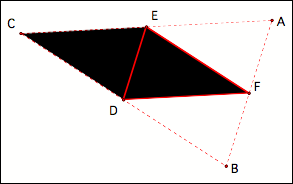
Summary: If you are given the Medial Triangle, the points of the original triangle may be found by “completing” parallelograms with that triangle.