EMAT 6680 :: Write Up #6 :: Clay Kitchings

Problem:

A parabola is the set of points equidistant from a line, called the directrix, and a fixed point, called the focus. Assume the focus is not on the line. Construct a parabola given a fixed point for the focus and a line (segment) for the directrix.

a. Use an Action Button to generate the parabola from an animation and trace of a constructed point.

b. Repeat 9a with a trace of the tangent line at the constructed point.

c. Use the locus command to generated the parabola from a constructed point or the tangent line at that point.

Part a) Use an Action Button to generate the parabola from an animation and trace of a constructed point.

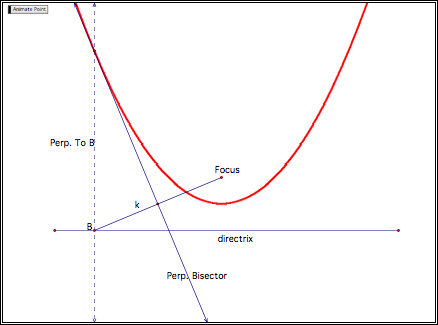
Picture (GSP):

The red curve (parabola) is formed by the traces of a constructed point. (Click the picture above to obtain your own GSP file and view the animation on your GSP program.)

Next (part b), let us trace the perpendicular bisector to the segment constructed from the Focus to the arbitrary point B along the directrix… shall we?

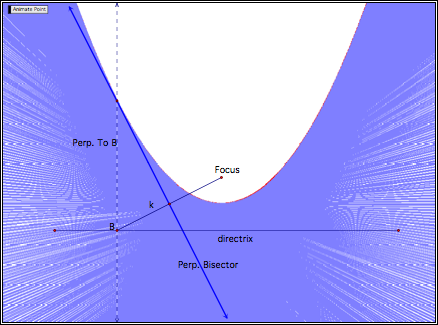
Now we have traced the perpendicular bisectors that form the tangent lines and thus define the shape of the parabola.

Next, we are to create a locus using the Locus command in GSP

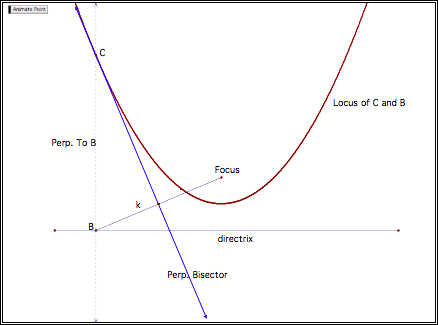
Now, just for the sake of curiosity and exploration, what would happen if we repeated the above “process” but instead used the Parabola as our “directrix?”

In order to accomplish this, we need to construct a segment from C to the original Focus. Then, our perpendicular line to the curve at any point is actually a perpendicular line to the original tangent line (in blue). We shall investigate what happens with the intersection of this perpendicular with the perpendicular bisector constructed to the segment joining C and the Focus. (The picture has been modified to fit in our screen.)

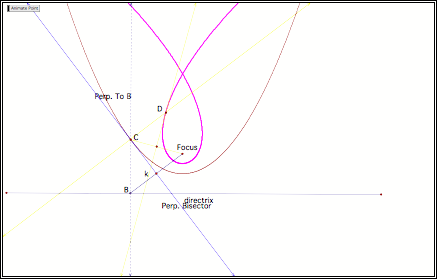
Using the Locus Command from the Construct Menu (with Points B and C), we observe somewhat of a “teardrop” shape, which continues to the right and to the left.