EMAT 6680 :: Assignment 11 :: Problem 1 :: Clay Kitchings

Investigate

Note:

· When a and b are equal, and k is an integer, this is one textbook version of the " n-leaf rose."

· Compare with

for various k. What if . . . cos( ) is replaced with sin( )?

***Note: For the purposes of working this problem, any ordered triple shall represent the values a, b, and k as (a, b, k).***

Unless otherwise noted,.

We shall begin with perhaps the most basic case: (1, 1, 1). The resulting graph is:

For now, we shall leave k=1 and modify a and b to see how this affects the graph.

(same as first graph above)

(new blue graph for a=2, b=2)

(The value k remains at 1 for now.)

It appears that when a = b the graph has a similar pattern each time. Furthermore, it appears that the a and b values have something to do with where the graphs intersect the x-axis.

Observation leads me to conjecture that “a-b” will be the opposite value of the x-intercept on the negative x-axis and “a+b” is the value of the x-intercept of the positive x-axis. Even if a<b, “a-b” will be a negative distance for the negative x-axis which would place the x-intercept on the positive x-axis and its opposite value (-[a-b]) will be positive. For example, if a=1 and b=2, consider the graph below.

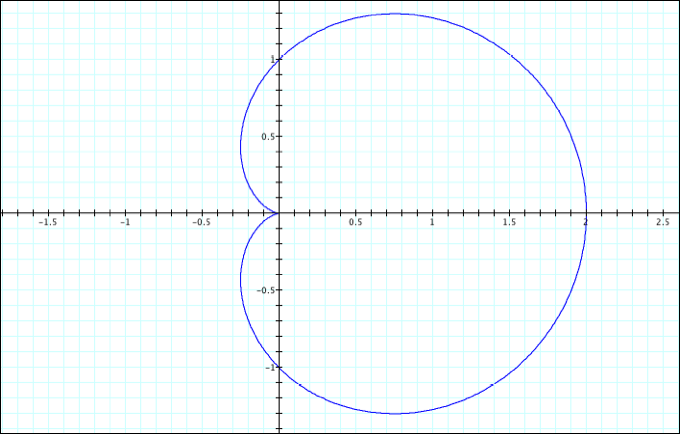
Values: (1, 2, 1)

So, notice a<b in this case. è a – b = -1, and its opposite is positive 1. For the a+b conjecture, a+b=3 and the graph intersects the positive x-axis at 3.

What happens if a and b are both less than zero?

(-1, -2, 1)

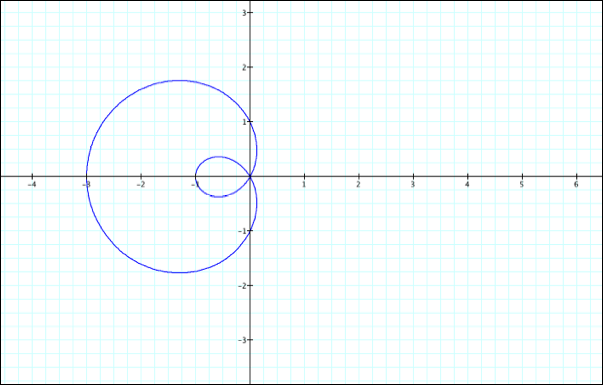
If a<0 and b<0, the graph is reflected over the y-axis.

If , then the graph does not loop within itself, but rather begins to “appear” more “circular” as the distance between and b increases (when ).

Now, let us modify the value of k for these kinds of graphs.

Fix a=b=1 and vary k to obtain the following graphs:

K=2:

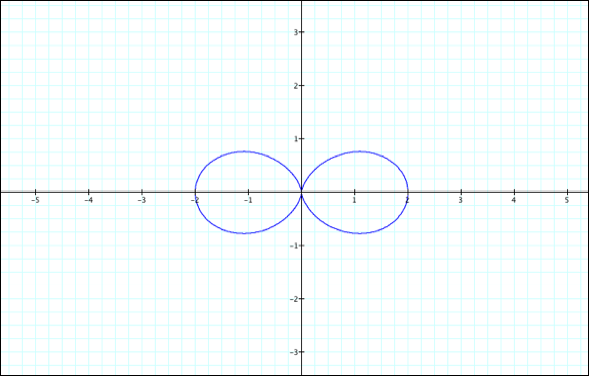
k=3

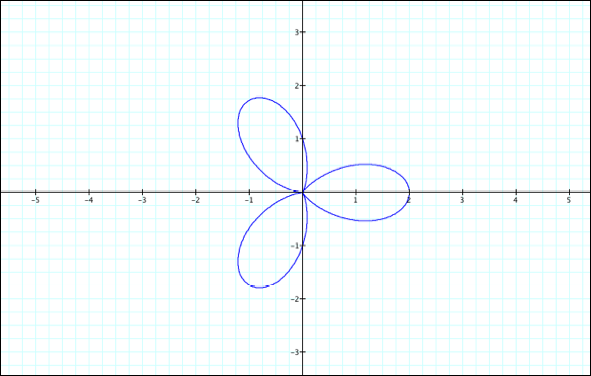
k=4

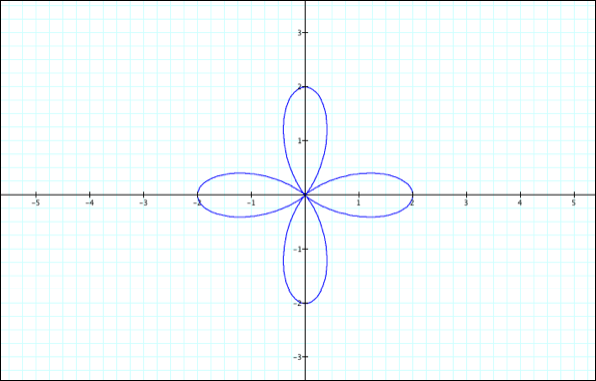
k=5

From the former three observations seem to imply that for a=b=1, the k-value will correspond to the number of “leaves” or “pedals” the graph has.

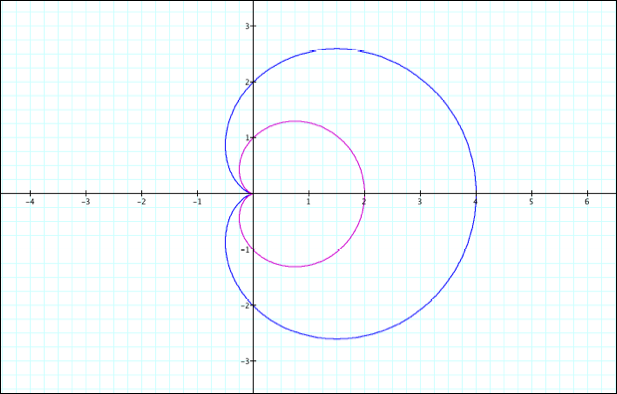
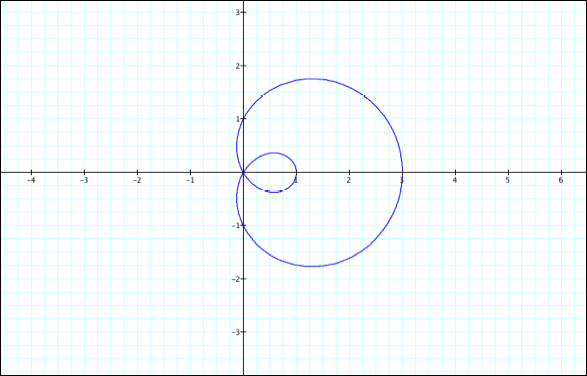
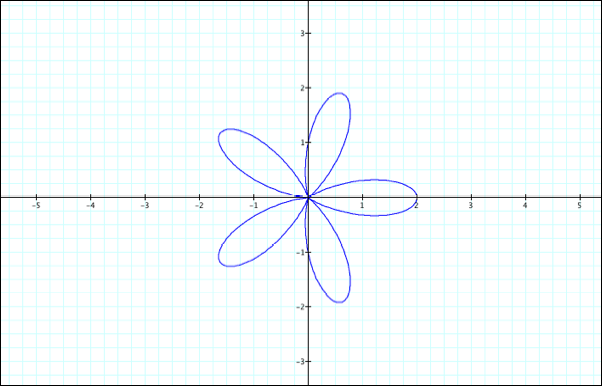
Now, let us fix a=1, k=5 and vary the value of b. At this point, we shall also fix a>0 and b>0

b=2

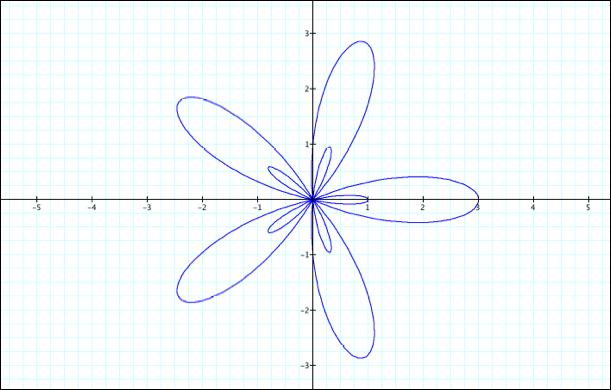
b=3

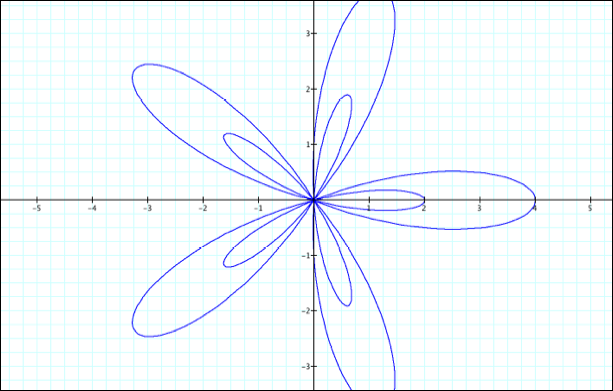
It appears that as long as a<b, another set of “pedals” (corresponding to k) forms within the outer “pedals.” What happens when a>b? At this point we shall fix b=1, k=5 and vary a.

a=3

a=4

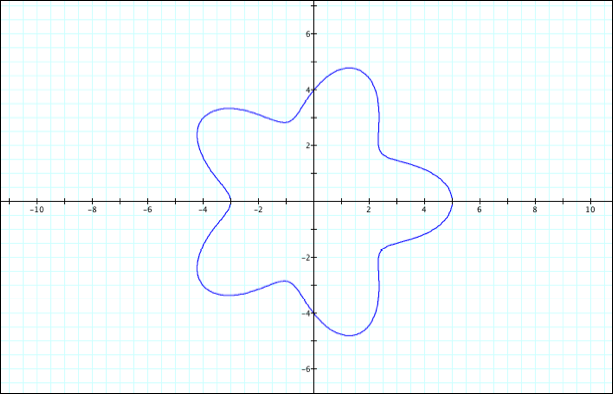
a=5

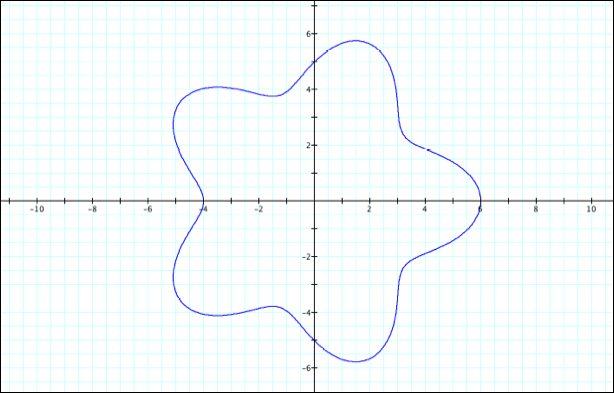
As we observed earlier in this problem there appears to be a relationship between a, b, and the left and right x intercepts. Notice that a-b appears to provide the left-most intercept on the x-axis and a+b provides the right-most x-intercept. As before, we see the a-value appears to correspond to the lower y-intercept (-a) and the upper y-intercept (a).

What happens if we observe the equation: ?

First we notice that as b increases, the size of the resulting graph from the k-value increases as well. So how do various values of k change the graph’s characteristics? For the purposes of this investigation, we shall fix b at 3.

We shall now compare the following graphs:

Green Red

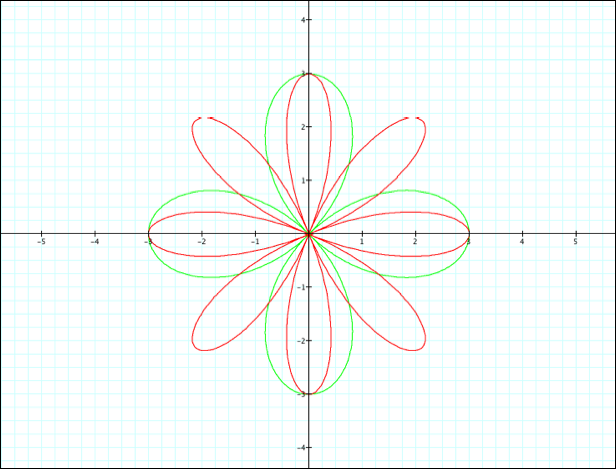
There appears to be a correlation between even k-value and the number of “leaves” or “pedals” that exist in the graphs. For example, the green graph has a k-value of 2 and contains four “pedals” whereas the red graph results from a k-value of 4 and has 8 pedals in it. From observing other even values for k, we conjecture that if k is even, there are 2k pedals in the resulting graph. For negative, even values of k, we observe identical graphs.

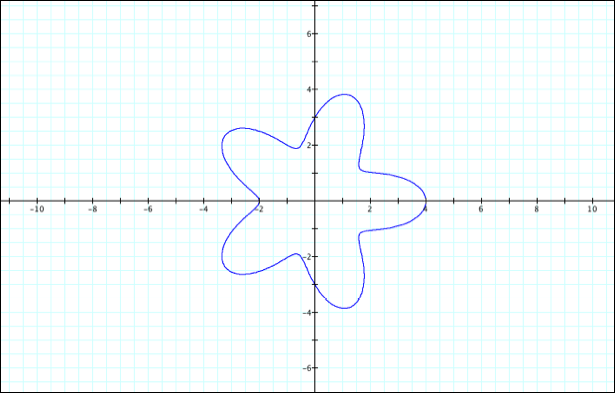
What happens when k is an odd value?

Using the same equation as the previous example, we will only modify k such that it takes on odd values. If k is odd, there are k “leaves” or “pedals” in the graph.

Example: k=5 (there are five pedals/leaves):

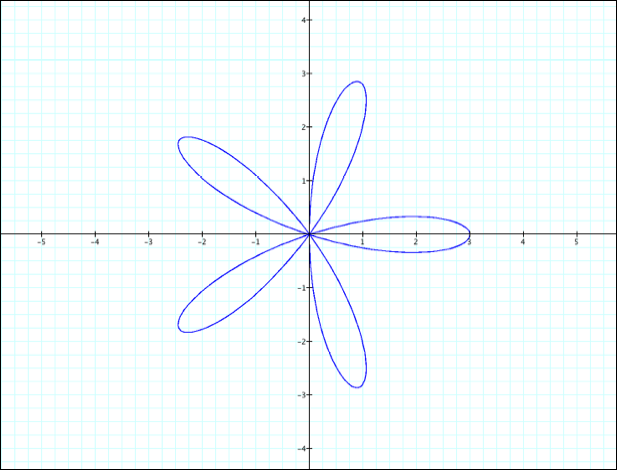
Finally, what might happen if we decided to use sine instead of cosine in these equations?

First, let us view the graphs of r = sin(bq) and r = cos(bq) in blue and red respectively. (k=2)

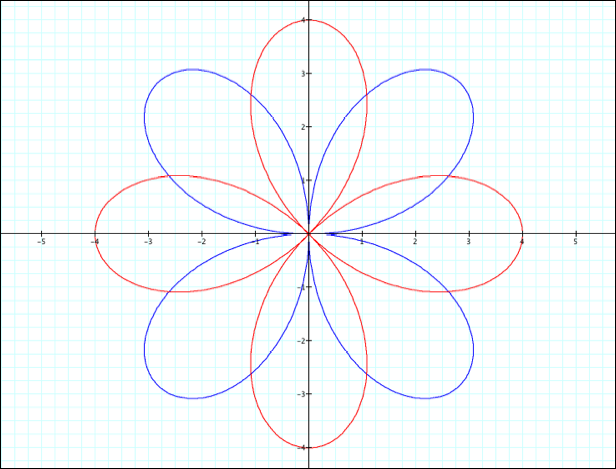
It appears that there is some kind of rotation going on, but this is only an observation for k=2. It would make sense that this might be rotated in some way since sine and cosine are shifts of each other.

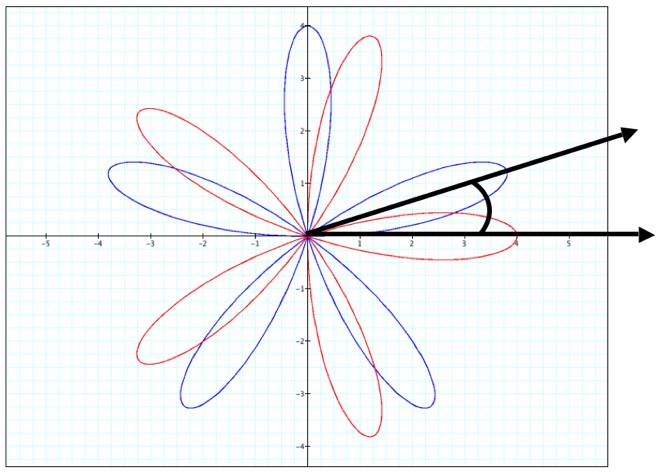
Let’s make k=4 and try it again…

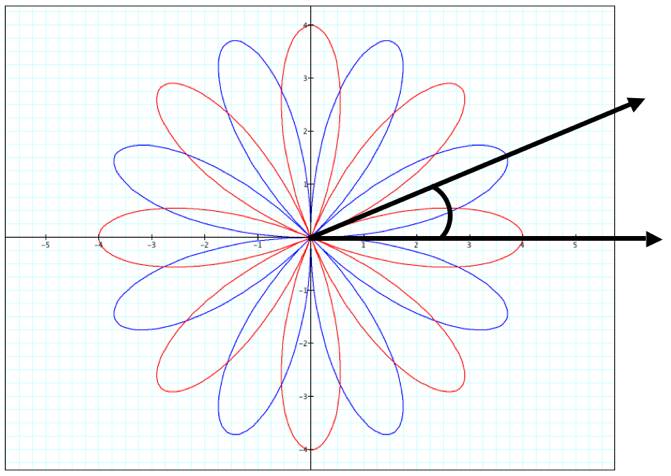
I have superimposed an angle between one pedal from cosine and one sine pedal. This angle is representative of a possible angle of rotation. For the even values of k, it is worth noting that this angle of rotation appears to be equivalent to 90/k (assuming a counter-clockwise rotation). Here, 90/4 = 22.5 degrees. Why four? Because four such superimposed angles would fit into 90 degrees.

Let us view this with an odd value for k and see if it appears to be true there as well.

If indeed 90/k provides the amount of the counter-clockwise rotation, then in this case the rotation would be 18 degrees.