EMAT 6680 :: Clay Kitchings :: Assignment 12 ::
Fibonacci Numbers
Exploring
Fibonacci Numbers
Generate
a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1, and f(n) =
f(n-1) + f(n-2).
*
= values begin with n=2
|
n |
|
ratios |
|
|
f(n-1)
+ f(n-2) |
*
f(n)/f(n-1) |
|
0 |
1 |
undefined |
|
1 |
1 |
1 |
|
2 |
2 |
2 |
|
3 |
3 |
1.5 |
|
4 |
5 |
1.666666667 |
|
5 |
8 |
1.6 |
|
6 |
13 |
1.625 |
|
7 |
21 |
1.615384615 |
|
8 |
34 |
1.619047619 |
|
9 |
55 |
1.617647059 |
|
10 |
89 |
1.618181818 |
|
11 |
144 |
1.617977528 |
|
12 |
233 |
1.618055556 |
|
13 |
377 |
1.618025751 |
|
14 |
610 |
1.618037135 |
|
15 |
987 |
1.618032787 |
|
16 |
1597 |
1.618034448 |
|
17 |
2584 |
1.618033813 |
|
18 |
4181 |
1.618034056 |
|
19 |
6765 |
1.618033963 |
|
20 |
10946 |
1.618033999 |
|
21 |
17711 |
1.618033985 |
|
22 |
28657 |
1.61803399 |
|
23 |
46368 |
1.618033988 |
|
24 |
75025 |
1.618033989 |
|
25 |
121393 |
1.618033989 |
|
26 |
196418 |
1.618033989 |
|
27 |
317811 |
1.618033989 |
|
28 |
514229 |
1.618033989 |
|
29 |
832040 |
1.618033989 |
|
30 |
1346269 |
1.618033989 |
It
appears that this sequence converges to approximately 1.61803989...
LetÕs
see if we can find an exact value for this approximation. First, letÕs assume that this sequence
does indeed converge to some 
. Take a ratio
for a high value of n as n approaches infinity.
The
sequence might appear as follows:
1,
1, 2, 3, 5, 8, É, a, b, a+b
Consider
the ratio: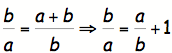 
If
the sequence converges, it must converge to some value 
=b/a (b/a is practically equal to (a+b)/b when n approaches +
infinity). This implies:
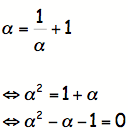
Now,
use the quadratic formula to solve:
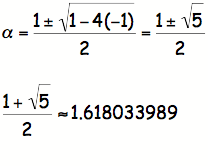
The
Fibonacci Sequence converges to 
.
If
we take different ratios, we can conjecture that other such ratios converge as
well (to different 
).
|
n |
|
ratios |
every 2nd ratio |
every 3rd ratio |
|
|
*f(n-1) + f(n-2) |
* f(n)/f(n-1) |
|
|
|
0 |
1 |
undefined |
|
|
|
1 |
1 |
1 |
|
|
|
2 |
2 |
2 |
2 |
|
|
3 |
3 |
1.5 |
3 |
3 |
|
4 |
5 |
1.666666667 |
2.5 |
5 |
|
5 |
8 |
1.6 |
2.666666667 |
4 |
|
6 |
13 |
1.625 |
2.6 |
4.333333333 |
|
7 |
21 |
1.615384615 |
2.625 |
4.2 |
|
8 |
34 |
1.619047619 |
2.615384615 |
4.25 |
|
9 |
55 |
1.617647059 |
2.619047619 |
4.230769231 |
|
10 |
89 |
1.618181818 |
2.617647059 |
4.238095238 |
|
11 |
144 |
1.617977528 |
2.618181818 |
4.235294118 |
|
12 |
233 |
1.618055556 |
2.617977528 |
4.236363636 |
|
13 |
377 |
1.618025751 |
2.618055556 |
4.235955056 |
|
14 |
610 |
1.618037135 |
2.618025751 |
4.236111111 |
|
15 |
987 |
1.618032787 |
2.618037135 |
4.236051502 |
|
16 |
1597 |
1.618034448 |
2.618032787 |
4.236074271 |
|
17 |
2584 |
1.618033813 |
2.618034448 |
4.236065574 |
|
18 |
4181 |
1.618034056 |
2.618033813 |
4.236068896 |
|
19 |
6765 |
1.618033963 |
2.618034056 |
4.236067627 |
|
20 |
10946 |
1.618033999 |
2.618033963 |
4.236068111 |
|
21 |
17711 |
1.618033985 |
2.618033999 |
4.236067926 |
|
22 |
28657 |
1.61803399 |
2.618033985 |
4.236067997 |
|
23 |
46368 |
1.618033988 |
2.61803399 |
4.23606797 |
|
24 |
75025 |
1.618033989 |
2.618033988 |
4.23606798 |
|
25 |
121393 |
1.618033989 |
2.618033989 |
4.236067976 |
|
26 |
196418 |
1.618033989 |
2.618033989 |
4.236067978 |
|
27 |
317811 |
1.618033989 |
2.618033989 |
4.236067977 |
|
28 |
514229 |
1.618033989 |
2.618033989 |
4.236067978 |
|
29 |
832040 |
1.618033989 |
2.618033989 |
4.236067977 |
|
30 |
1346269 |
1.618033989 |
2.618033989 |
4.236067978 |