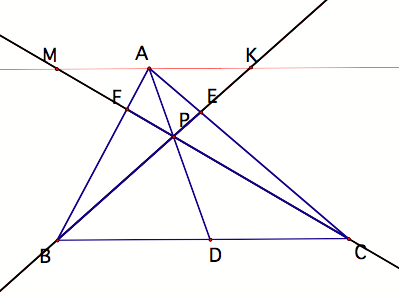
Clay Kitchings :: EMAT 6680 :: CevaŐs Theorem :: Final Write Up Part B
Ceva's
Theorem. Consider any triangle ABC. Select a point P inside the triangle and
draw lines AP, BP, and CP extended to their intersections with the opposite
sides in points D, E, and F respectively.
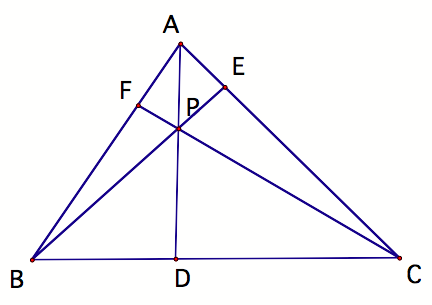
It
is worth noting that segments BE, AD, and CF may be referred to as Cevians.
We
shall first explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and
various locations of P.
According to our investigation with GSP, we
find that these two expressions are actually equal for various locations of P
inside triangle ABC. Now we shall attempt to verify this conjecture.
After
several attempts at finding similar triangles using auxiliary lines, I finally
found some that were helpful. Construct a line (L1) through A that is parallel
to segment BC. Extend lines FC and
BE so that they intersect L1 at M and K respectively. (To obtain a GSP sketch, click the figure below.)
The
alternate interior angles and vertical angles give us AA similarity for
numerous pairs of triangles. I shall highlight two of them as examples and then
list the others. Triangle KPA is similar to triangle BPD by AA similarity
(vertical angles and alternate interior angles).
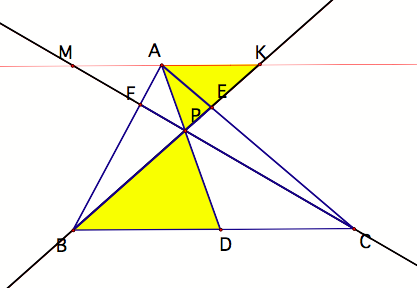
Similarly
(pardon the pun), the following triangles are similar:
(a)
Triangles MPA and CPB
(b)
Triangles KPA and BPD
(c)
Triangles MAP and CDP
(d)
Triangles KEA and BEC
(e)
Triangles CFB and MFA
As
a result of the similar triangles, we may now write the following proportions:
1) ![]() 2)
2)
![]() , 3)
, 3)
![]() , 4)
, 4)![]()
From
the last two proportions, we may write the following proportion (via
substitution):
5) ![]() 6)
6) ![]()
Now
letŐs consider these three proportions and manipulate them a little with some
algebra:
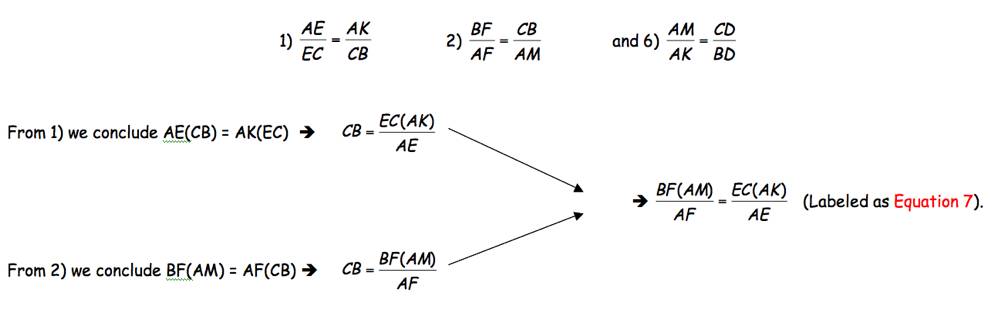
From
Equation 7, we may write the following:
EC(AK)(AF) = AE(BF)(AM)
Now,
let us divide both sides by AK, simplify, and substitute (using #6 above):
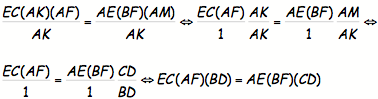
Now
we have shown that for segments (Cevians) constructed within a triangle such
that they are concurrent, the relationship above holds. Is the converse true? In other words,
if cevians of the triangle form the equivalence above, does this imply that the
segments are concurrent?
First,
we shall assume that in triangle ABC, segments BE and CF intersect at P (on the
interior of triangle ABC). Let point D exist such that AF(BD)(CE) =
BF(CD)(AE). Now also construct
Cevian ADŐ through point P.
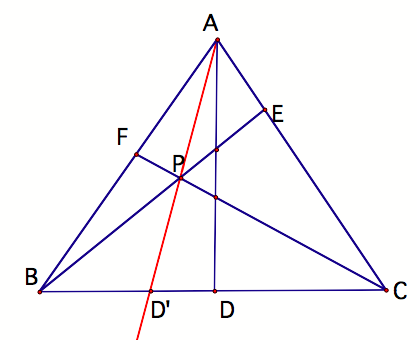
From
the previously proved conjecture, we now know AF(BDŐ)(CE) = BF(CDŐ)(AE). Now we form the relationship via
substitution:
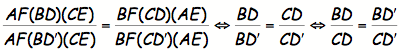
Since
the ratio of BD:CD = BDŐ:CDŐ, this implies DŐ=D, which further implies that AD,
CF, and BE are concurrent at point P since point P lies on ADŐ.
Conclusion:
For
any triangle ABC, AF(BD)(CE) = BF(CD)(AE) if and only if segments BE, CF, and
AD are concurrent.
What
if point P is on the exterior of triangle ABC? Click here for a GSP
demonstration of this case. A
proof for such a case would be comparable to the case with P inside the
triangle, and would involve using similar triangles as before.
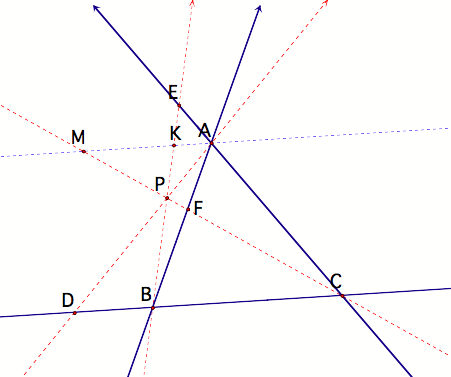
CevaŐs
Theorem allows us to prove points of concurrency for triangle medians, angle
bisectors, and altitudes. However, we have to be a bit cautious concerning the
intersection of the perpendicular bisectors because they only pass through the
vertices of the triangle on special occasions, and thus would not fall under
the definition of a Cevian.