Clay Kitchings :: EMAT 6600 :: Minimum of

Use the AM-GM inequality to show that the minimum of is 2.

AM-GM Inequality:

Let a = 1/x and b = x

Apply AM-GM Inequality

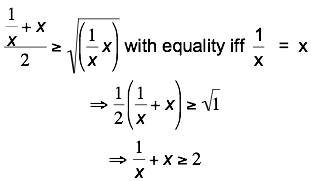
Now for the “with equality” part: 1/x = x implies x =1 or -1. The negative value does not satisfy the above inequality, but x=1 satisfies it. So let’s calculate f(1). f(1) = 1/1 + 1 = 2. So, this value will always be larger than or equal to 2, so therefore the minimum of the function is indeed 2.