April 18, 2007

*Ball floating in mercury problem.

*D is the area of the “slant triangle.”

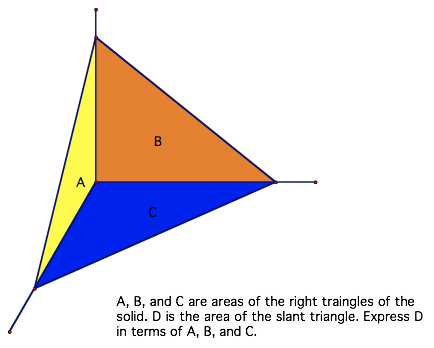
This gives an analog of the Pythagorean Relationships.

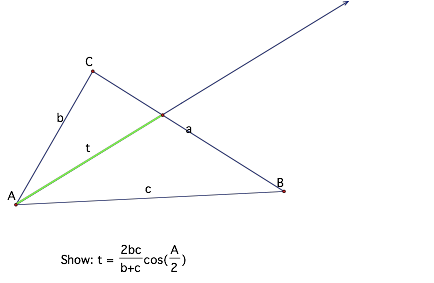
Note the extensions via rays in the following part of the same figure:

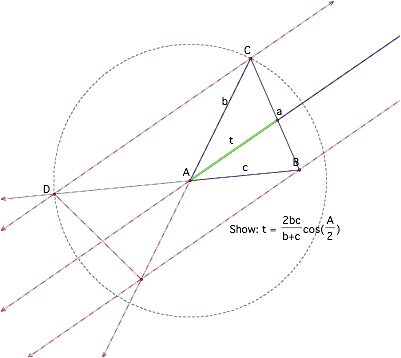
Show that D and C are equidistant from A.

*Note: Stewart’s Theorem gives the above relationship regardless of whether or not the “t” segment is an angle bisector. (The proof requires using triangle areas).

A man walked for five hours, first along a level road, then up a hill, then he turned around and walked back to the starting point along the same route. He walks 4 mph on the level ground, 3 mph up the hill, and 6 mph downhill. Find the distance walked.

Claim: When you get a solution for this, if you change the numbers above, you’ll not get the solution.

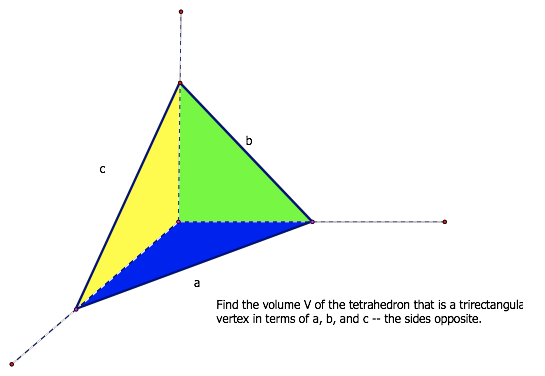
http://jwilson.coe.uga.edu/EMT725/Bob2/RtTri.html

Not hard to show that this must be a right triangle via algebraic manipulation, but how could you show it geometrically?

S₁ = 1 + 2 + 3 + … + n

S₂ = 1² + 2² + 3² + 4² + … + n²

S₃ = 1³ + 2³ + 3³ + … + n³.

Show that S₃ = S₁².

Find the length of the curve that passes through each of the three points:

http://jwilson.coe.uga.edu/EMT725/grass/grass.html

If 6 acres of grass, together with what grows on the 6 acres during the time of grazing, keep 16 oxen for 12 weeks, and 9 acres keep 26 oxen 9 weeks, how many oxen will 15 acres keep 10 weeks, the grass growing uniformly all the time?

Grass Consumption by Oxen Problem

a = amount of grass per acre at start

g = amount of grass per acre that grows per week.

x = amount of grass eaten by one ox per week

amount eaten plus amount that grows back = amount of grass 16 oxen eat in 12 weeks

6a + 12*6g = 16*12x

9a + 9*9g = 26*9x

15a + 10*15g = y*10*x

Divide through by x (because these are rates):

6k + 12*6m = 16*12

9k + 9*9m = 26*9

15k + 10*15m = 10y where k = a/x and m = g/x

http://jwilson.coe.uga.edu/EMT725/Isos.Trpzd/sin.cos.html