March 28, 2007 :: EMAT 6600 :: Problem Solving Class Notes

About Parabolas…

Are these parabolas “parallel” to teach other? What does it mean for two curves to be parallel? Does it mean that the tangent lines at each x value are parallel on both curves?

They will always be 10 units apart on the vertical sense of distance.

∆d

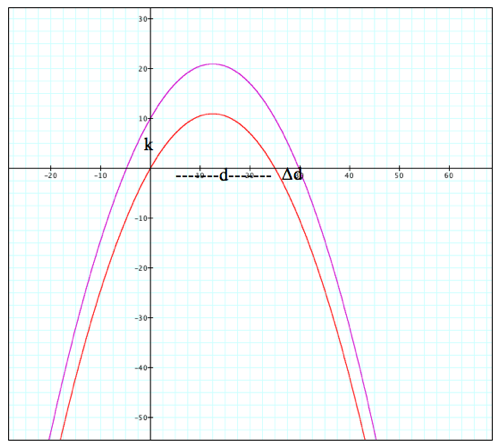
Adding a constant just moves the parabola up and down.

Problem, express ∆d in terms of k and d.

∆d = 5 (approx.), k=10 d=25

This is the model of a “real-life application.” On some of the driving ranges (for people who enjoy something like golf). At a driving range, you may be up on a platform when you drive the ball. Knowing this ∆d will help determine how far you actually drove the ball.

To solve:

Express the “lower” curve as f(x) = -ax(x-d) + k and the “upper” curve as g(x) = -a[x-(d+∆d)] [x + ∆d]. If we equate f(x) and g(x), we’ll be able to solve for ∆d.

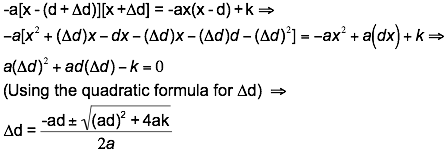
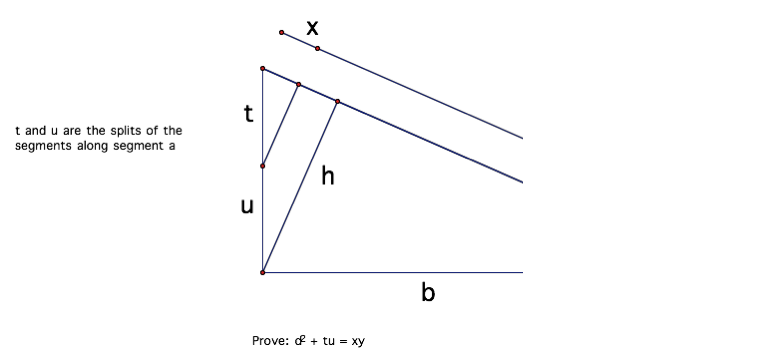
Discussion about looking at (or for) some application of the Geometric Mean within this problem.

Another problem:

Next Problem:

120 degree Triangle.

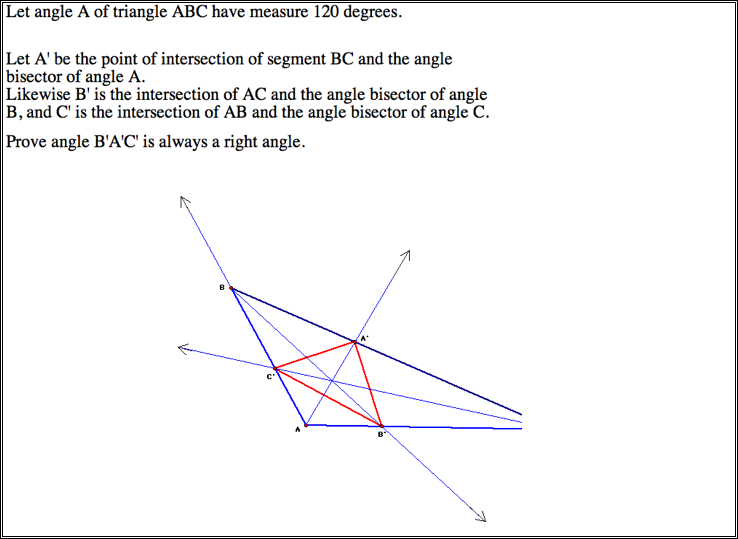
This is NOT going to be an isosceles right triangle. Claim: the ratio of BA/AC = AB’(B’C) – may be helpful in proving this problem. (Consider incircle as well.)