Ratio on a Line Segment :: Clay Kitchings :: EMAT 6600 :: Spring 2007

Return to Clay’s 6600 Page

Tell Clay what a buffoon he is

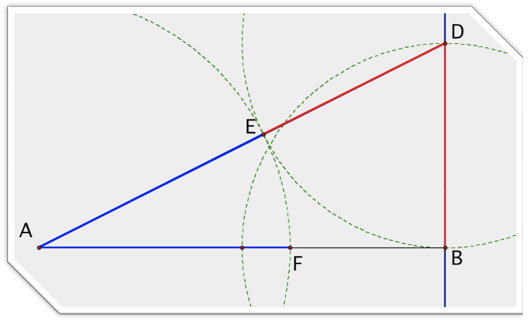
Given the following construction where AB = 2DB, DB = DE, and AF = AE, find AF/BF.

(From http://jwilson.coe.uga.edu/emt725/Ratio/ratio.html)

I spent several hours doing some algebraic manipulations on the relationships I knew. I started with the Pythagorean relationship, but went too far at first by expanding each squared term (such as AB² = (AF + BF)², etc. After a while of getting nowhere, I decided to redo the algebraic manipulation behind the Pythagorean relationship as follows:

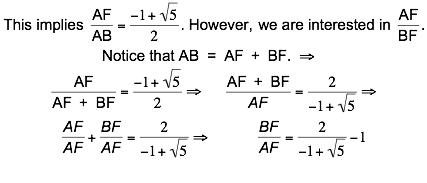
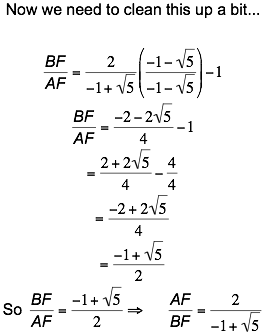
What guided me during this process and what did I learn? I learned that it is helpful to continually monitor what I’m doing and check for the end result. I knew from the hint in the problem that “something golden” would come out of this somewhere, most likely. I also learned that it is often helpful to substitute something like “x” for some “messy” terms to make things look more familiar. I knew the typical quadratic that can give the golden ratio, so I kept looking for ways to get something of the form x² + x – 1 = 0. I also highly suspected it would be nice to keep AF and AB in the manipulations, even if I was unsuccessful at keeping BF in there. I knew that BF was included in AB and I suspected I could find BF if I had AB in there the whole time.