Clay Kitchings :: EMAT 6600 :: Divisibility

 

 

Again, this problem arose from curiosity about rules of divisibility for various integers in MATH 6000.  Where do rules for divisibility come from?  How did ÒtheyÓ come up with them? (And who on earth is/are ÒtheyÓ anyway?)

 

Rules for divisibility come from ÒexpandingÓ numbers and writing them almost as if they were polynomials. For example, one can think of 2532 as the following:  .

 

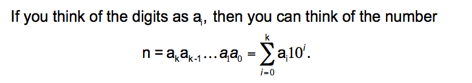
:::::::Desktop:Picture 2.png

 

 

 

Problem: Generate the rule for divisibility by 11.

 

Some experience with modular arithmetic comes in handy for this derivation. We shall apply some properties of modular arithmetic and see what happens:

 

 

:::::::Desktop:Picture 3.png

 

 

 

 

 

Now, apply the definition of congruence in modular arithmetic:

 

 

 

 

 

 

 

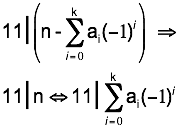
But, what does this summation really mean? It means:

 

 

 

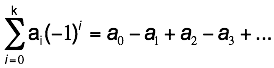
Basically, it is a +/- alternating ÒsumÓ of the digits.  So, 11|n if and only if 11 divides the Òalternating sumÓ of the digits.  Here is an example:

 

Is 3417524 divisible by 11?

 

Check:  4-2+5-7+1-4+3 = 0, which is certainly divisible by 11. Therefore 3417524 is divisible by 11.