Clay Kitchings :: EMAT 6600 :: Counting the Triangles II

http://jwilson.coe.uga.edu/EMT725/Bob/Count.Triangles.II.html

Count the triangles: Extend the sequence:

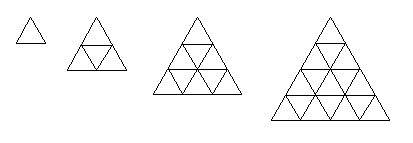
So far, we have 1, 5, 13, and 27. Why are we getting these numbers? Are there “hidden” patterns within these numbers?

Let’s look at the n=4 case (the fourth one in the picture above).

We shall methodically count the number of triangles of various sizes based on what I’ll call the “size of the base.” For example, the size of the base of the largest triangle for n=4 is 4. That one large triangle has a base size of 4 for these purposes.

We’ll create a table of values for the triangles that are pointed up as well as down

For n = 4:

Base Size (oriented “up”)	Number of Triangles
4	1
3	3
2	6
1	10

This 1, 3, 6, 10 sequence is extremely likely to form the entire triangular number sequence. At this point, I am at least suspicious that triangular numbers might be involved.

Base Size (oriented “down”)	Number of Triangles
4	0
3	0
2	1
1	6

If we add the number of triangles from each table, we do indeed get 27 total distinct triangles.

Now, let’s look at the n=5 case:

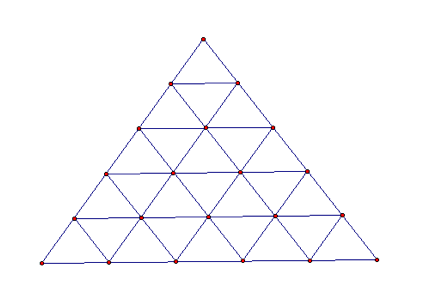
Base Size (oriented “up”)	Number of Triangles
5	1
4	3
3	6
2	10
1	15

Base Size (oriented “down”)	Number of Triangles
5	0
4	0
3	0
2	3
1	10

So, for n = 5, we can count 48 distinct triangles.

Let’s now consider n=6 and do a little more counting:

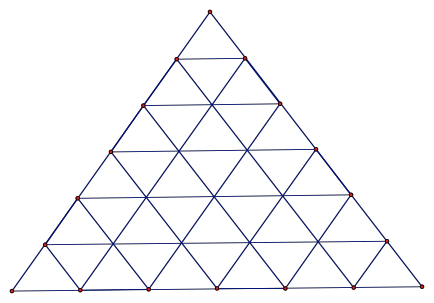
Base Size (oriented “up”)	Number of Triangles (up)
6	1
5	3
4	6
3	10
2	15
1	21

No surprises here with the triangles oriented “up.” The issue is a question about those triangles oriented “down.”

Base Size (oriented “down”)	Number of Triangles (down)
6	0
5	0
4	0
3	1
2	6
1	15

Up + Down = 56 + 22 = 78

Let’s continue to investigate by going to n = 7:

Base Size (oriented “up”)	Number of Triangles (up)
7	1
6	3
5	6
4	10
3	15
2	21
1	28

Base Size (oriented “down”)	Number of Triangles (down)
7	0
6	0
5	0
4	0
3	3
2	10
1	21

So for n=7, we have 84 + 34 = 118

Consider also n=8:

It is no longer a mystery from my perspective concerning the triangles that are oriented in the “up” direction. They are the sum of the first n triangular numbers. So in this case, we’re talking about the sum of the first 8 triangular numbers. In the n=8 case, the sum of the first 8 triangular numbers is 120.

What would be nice is to figure out what is going on with the downward-pointing triangles.

Base Size (oriented “down”)	Number of Triangles (down)
8	0
7	0
6	0
5	0
4	1
3	6
2	15
1	28
Total	50

Conjecture: The number of triangles oriented down for a triangle with base size of n will be some type of sum of odd numbered triangular numbers. In the example of n=8, we see the triangular numbers 1, 6, 15, and 28, which are the first, third, fifth and seventh triangular numbers.

After going back and looking at the other trends for the downward totals, I have the following conjecture (in two parts):

· it appears that if n is odd, then the number of downward pointing down is the sum of the first even triangular numbers (second + fourth + … + (n-1)th )

· it appears that if n is even, then the number of downward pointing triangles is the sum of the first odd triangular numbers (first, third, fifth, … + (n-1)th )

In order to generate each of the first n-even triangular numbers (even for the n-values such as n=2, n=4, n=6, etc., for some natural number k), I substituted k=2n into the formula I knew for triangular numbers: . Beginning with T(1),..., we obtain the sequence of triangular numbers generated by even integers {3, 10, 21, 36, 55, …}.

In order to generate each of the first n-odd triangular numbers (such as n=1, n=3, n=5…) we consider the function where m=2n-1 for natural numbers, n. This will generate the sequence of the triangular numbers from odd n-values.

So, for now, we have a “rough shell” of a formula for counting all the triangles for the nth case:

Total number of triangles = Number of upward triangles + number of downward triangles

Let T(n) be the number of total triangles in the figure.

Then T(n) = (Sum of the first n triangular numbers) + (Sum of the downward triangles)

This problem is still in progress. I wanted to document the work I have done so far with it. I hope to complete it more as time goes on and I gain more insight into it.