The Triangle Midsegment Theorem:

“In a triangle, the segment joining the midpoints of any two sides will be parallel to the third side and half its length.”

Consider the triangle below:

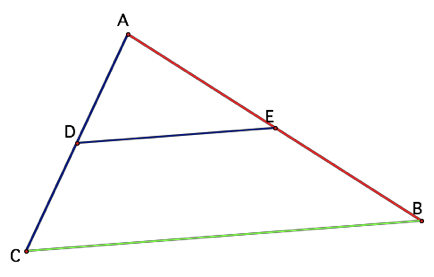
Construct a line through C that is parallel to AB.

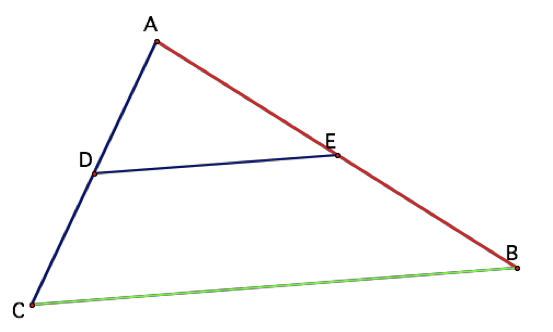
We know the following equalities by the midpoint construction:

AD = DC and AE = EB. We can use the reflexive property of equality for angle A to obtain a SAS similarity of triangles DAE and CAB. Now that the two triangles are congruent, we have m<ADE = m<ACB. By the converse of the Corresponding Angles Theorem, we have DE || CB.

Now we need to show that DE = ½ CB.

Claim: Quadrilateral CBEF is a parallelogram. If we can show FC=EB, we can conclude that CBEF is a parallelogram.

*(side): We have m<FCD = m<EAD by the Alternate Interior Angles Theorem

*(angle): We have AD = DC (from above – definition of midpoint)

*(side): We have m<FDC = m<ADE by the Vertical Angles Theorem.

**We now have Triangle FDC is congruent to Triangle EDA by the SAS Congruence Theorem.

Therefore, FC = AE --> FC = EB. If a pair of opposite sides of a quadrilateral are both congruent and parallel, then the quadrilateral is parallelogram (previous theorem). Therefore FE = CB. Also, the above triangle congruence gives us FD = DE.

Write: FE = FD + DE --> FE = 2DE --> DE = ½ FE

Since FE = CB, we can substitute: DE = ½ CB.

Therefore the Midsegment is half of the measure of the third side.

Conclusion: If the midpoints of any two sides of a triangle are joined by a segment, then that segment is parallel to the third side and half its length.