12 Favorite Problems

Carol Love

EMAT 6600

 

Link here for GSP file of these problems.

 

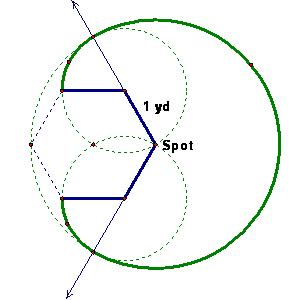
1.      Spot’s doghouse has a regular hexagonal base that measures on yard on each side. Spot is tethered to a vertex with a two-yard rope. What is the area, in square yards, of the region outside the doghouse that Spot can reach? (100 Favorite Calendar Problems #22)

 

The area of the reachable area is two-thirds of the two-yard circle plus two one-sixth sectors of the one-yard circles.

 

 square yards

 

 

 

 

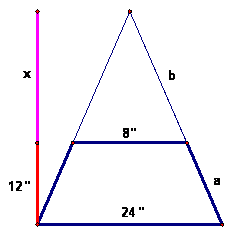
2.      Carl’s Cone: Make a pattern for a sawed off cone that is 12 inches tall, has a base diameter of 24 inches, and a top diameter of 8 inches.

 

First, x is the missing additional height of the original triangle. To find x, use a proportion with similar triangles.

 

    

 

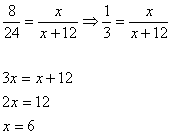
Now, b is the inner radius of the pattern. To find b, use the Pythagorean Theorem.

 

          

 

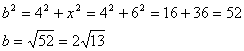
Next, l = a + b is the outer radius of the patter. To find l, use a proportion with similar triangles.

 

 

 

 

 

 

Now, construct the concentric circles with radii b and l ( and ).

 

 

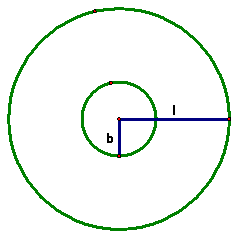
The length of the arc along the larger circle must be equal to the circumference of the bottom of the cone, or 24π. The circumference of the larger circle is . The central angle, θ, intersecting the arc must be in the same proportion to 2π as the length of the arc is to the circumference of the larger circle.

 

 

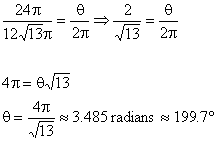
Therefore, the pattern is as follows, with an inner radius of , an outer radius of , and a intercepted arc of 199.7º.

 

 

3.      Oil Tank Problem: A cylindrical oil tank with a radius of 18” and a depth of 48” is filled such that there are 10” of oil in the tank. What volume of oil is in the tank?

 

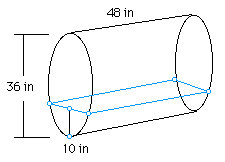
The volume of the entire tank is  in3. To find the volume of the remaining oil, construct a cross-section of the tank.

 

 

To find θ, the central angle intersecting the arc where the oil contacts the tank, we need the cosine ratio.

 

 

 

 

 

 

 

 

 

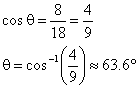
The oil fills the area of the sector that is 2θ less the area of the isosceles triangle. The area of the 2θ sector is

 

 

 

The area of the isosceles triangle depends on x.

 

 

 

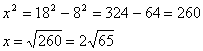
So, the area of the isosceles triangle is

 

 

 

Next, the area of the oil is  square inches. Multiplying by the depth, the volume of oil remaining is  cubic inches. Finally, since there are 0.004329004 cubic inches in a gallon, there are gallons of oil remaining.

 

 

 

 

 

 

4.      Each of the small circles in the figure has radius 1. The innermost circle is tangent to the six circles that surround it, and each of those circles is tangent to the large circle and to its small-circle neighbors. Find the area of the shaded region, yellow below. (100 Favorite Calendar Problems #23)

 

 

The area of each small circle is .

 

Because the diameters of three small circles form the diameter of the large circle, the diameter of the large circle is 6, making the radius of the large circle 3. The area of the large circle is, therefore, . The yellow area is the area of the large circle less the combined area of the seven smaller circles, or .

 

5.      Pick a point P on the inside of a unit square. Connect P with the vertices of the base of the square. What is the probability that the triangle so completed will be an acute triangle?

 

 

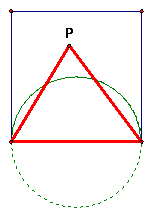
The triangle is a right triangle when P is on the 3 non-base sides of the square and when P is on the circle. Only angle P can be obtuse, and it is such when P is within the semicircular region. The probability of the triangle being acute can be found using an area model and finding . The area outside the semicircle is found by subtracting the area of the semicircular region from the area of the square. The area of the semicircular region I is , so the area outside the semicircle is . Therefore the probability of an acute triangle is .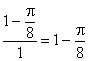

 

 

6.      A circle’s diameter is divided in the ratio of 3 to 4, and semicircles are drawn on each segment, as shown. What is the ratio of the upper area to the lower area? (100 Favorite Calendar Problems #32)

 

 

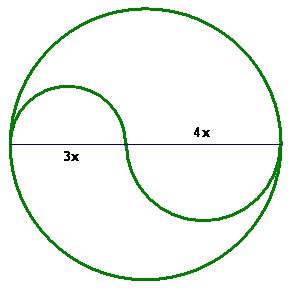
The upper area is one-half the large circle (diameter 7x) plus one-half of a circle of diameter 4x less one-half of a circle with diameter 3x.

 

 

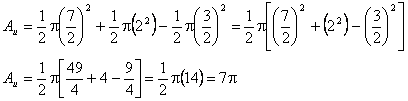
The lower area is one-half the large circle plus one-half of a circle with diameter 3x less one-half of a circle of diameter 4x.

 

 

Therefore, the ratio of the upper area to the lower area is

 

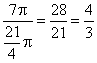
7.      Magic Square: Arrange the numbers 1 through 9 in a 3 by 3 array – a Magic Square – such that the sum of any row, column, or the two diagonals is the same.

 

8

1

6

3

5

7

4

9

2

 

This result is unique in that the only other solutions involve rotations or reflections of this solution. The five must be used in the greatest number of sums, and must therefore be placed in the center square. The 4-5-6 combination must be used on the diagonal and determines the sum of the rows, columns, and diagonals. The 1 and 9 are the upper and lower limits of the numbers, and must be used in a row or column, and together. The higher number should sum with the 4 and the lower with the 6.

 

Other 3 by 3 magic squares can be found as linear combinations of this original magic square. For instance, a magic square with 21 at the center is a 4(original square) + 1, and yields

 

33

5

25

13

21

29

17

37

9

 

using the numbers 5, 9, 13, 17, 21, 25, 29, 33, 37, which are of the form 4x + 1, where x is the original numbers 1 – 9.

 

A different magic square with 21 at the center can be formed using x + 16, and the numbers 17 – 25, as shown.

 

 

24

17

22

19

21

23

20

25

18

 

 

Here is a 4 by 4 magic square using 1 – 16.

 

1

2

15

16

13

14

3

4

12

7

10

5

8

11

6

9

 

8.      The figure is composed of twenty-five unit squares. What is the area of the unshaded region?

 

 

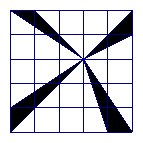
The unshaded region is composed of 4 triangles. The area of the top triangle is , the area of the right-side triangle is, the area of the bottom triangle is , and the area of the left-side triangle is . The area of the unshaded region is the sum of these four areas, or 4 + 4 + 6 + 6 = 20 square units.

 

 

9.      Let C be a cube where the length in inches of its long diagonal is the same as its volume in cubic inches. What is the length in inches or each side? (100 Favorite Calendar Problems #16)

 

 

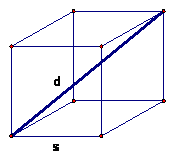
The length of the longest diagonal is . The volume of the cube is s3. So,

 

 

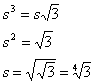
10.  A strip of uniform width is cut from three sides of a square region, leaving a rectangular region with are that is one-half that of the square region. Determine the quotient of the square length divided by the strip’s width. (100 Favorite Calendar Problems #20)

 

 

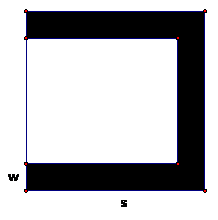
The area of the square is s2, so the area of the rectangular region is . The dimensions of the rectangular region are s – w and s – 2w. Therefore the area of the rectangular region is , and

 

 

So, either , which leads to

 

 

or , which leads to

 

 

Since the strip is cut from the square, the width of the strip must be shorter than the side of the square, leading to the choice of .

 

 

11.  If the perimeter of an isosceles triangle is 36 cm, and the altitude to its base is 12 cm, what is the triangle’s area? (100 Favorite Calendar Problems #25)

 

 

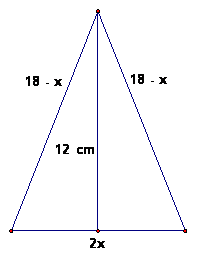
Checking to ensure the perimeter is correct,

2x + (18 – x) + (18 – x) = 2x + 36 – 2x = 36.

 

Now, x can be found using the Pythagorean Theorem.

 

 

So, the area of the triangle is  cm2.

 

 

 

12.  A square is inscribed in a semicircle as shown. Find the ratio of s to a. (100 Favorite Calendar Problems #90)

 

 

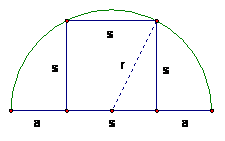
The radius, r, of the semicircle is found using the Pythagorean Theorem.

 

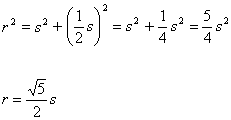
And a = r – s, so

 

 

 

Finally,