Investigations
Compass and Straightedge Constructions
First,
look at the tools for geometric constructions. The only tools that may be used
are a compass and a straightedge, or their software equivalent (such as the linear
and circle tools in Geometer’s Sketchpad). Ideally, the compass is collapsible,
such that a distance cannot be marked and moved to another location, but the
distinctions between the collapsible and non-collapsible compass are equivalent
after proving
The objects (elements) of construction are points, lines, segments, rays, and circles.
Basic Constructions
Copy a Segment
To copy a given segment, construct a point and use the compass to construct a circle with a radius equivalent to the length of the original segment. Any segment constructed as a radius of the circle will be congruent to the original segment. To view the interactive Java Sketchpad version, click here.
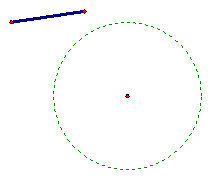
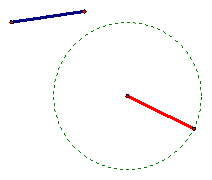
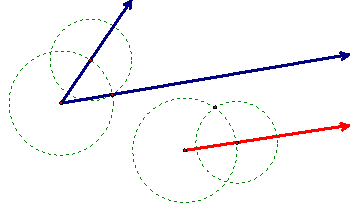
Copy an Angle
To copy a given angle, first construct a circle and the intersection points of the circle and the two rays forming the angle. Next, construct a circle with one of the intersections points as its center and the other defining the radius.
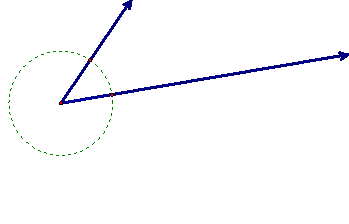
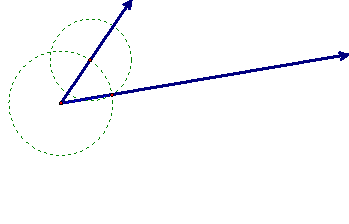
Now, construct a ray and a circle with the same radius as the original circle, marking the intersection of the circle and the ray. Then construct a circle with an equivalent radius to the second circle and mark the intersection of the two circles. Finally, construct a ray using the endpoint of the first ray and the final intersection point. To view the interactive Java Sketchpad version, click here.
Perpendicular Bisector
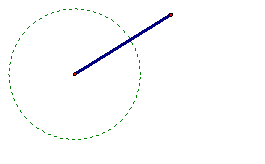
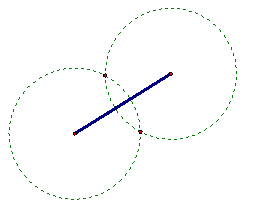
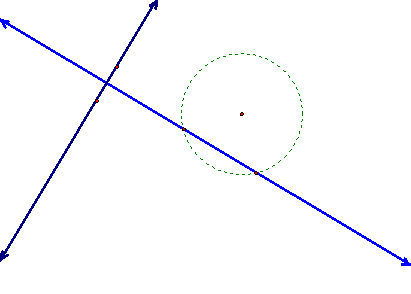
To construct the perpendicular bisector of a given segment, construct a circle centered at one endpoint with radius greater than half the original segment. Construct a circle centered at the other endpoint with the same radius, and the intersections of the two circles. The line constructed through the two intersections is the perpendicular bisector of the original segment. To view the interactive Java Sketchpad version, click here. The construction of a perpendicular bisector also allow for the construction of perpendicular lines.
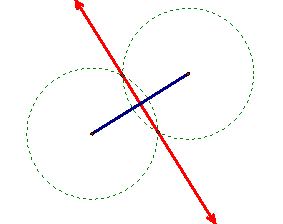
Angle Bisector
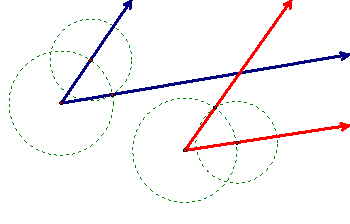
To construct the angle bisector of a given angle, construct a circle centered at the angle’s vertex and the intersections of the circle and the two rays forming the angle. Next, construct congruent circles using these intersection points as their centers, being sure the circles overlap. Then construct the intersections of the two circles. Finally, construct a line through the circles’ intersections. To view the interactive Java Sketchpad version, click here.
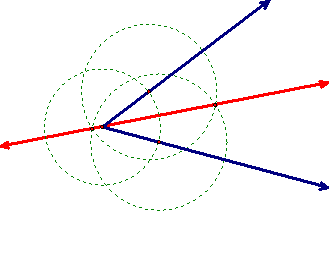
Parallel Lines
A line can be constructed parallel to a given line through a given line as follows. First, construct a point (typically, not on the original line, but could be used for the line containing given segment). Next, construct a line perpendicular to the original line (as a perpendicular bisector to a segment of the line). Finally, construct a line perpendicular to the perpendicular bisector through the constructed point by constructing a circle with the constructed point as its center, and using the intersections of this circle with the perpendicular bisector as a segment whose perpendicular bisector can be created. To view the interactive Java Sketchpad version, click here.
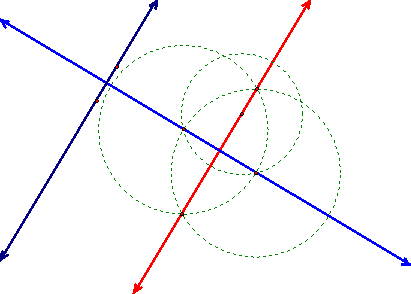
Investigations
Constructible Lengths – Given a unit length (one), what lengths (numbers) can be constructed?
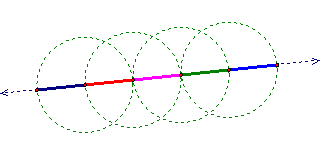
Without much fanfare, the natural numbers can be constructed. If the unit length (one) can be copied, then two can be constructed. If two can be constructed, then three can, etc. Therefore, by induction, the natural numbers are constructible. Shown below is a construction of the numbers 1 – 5. Similarly, the multiples of any constructible number are constructible. To view the interactive Java Sketchpad version, click here.
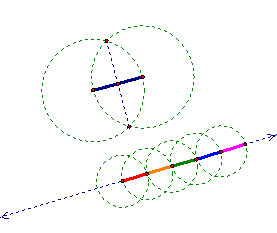
Rational numbers are also not too
difficult to construct. Multiples of 
are particularly
simple given the construction of the perpendicular bisector of a segment, which
divides the segment in half. Once 
is constructed, it can
be copied, leading to all the multiples of , the first five of which are shown below. To view the
interactive Java Sketchpad version, click here.
However, 
is not the only constructible rational number. In fact, all
rational numbers are constructible using similar triangles. The construction of
and 
are shown below. The
red segments are the rational segments and . Only rational numbers with prime denominators are shown
because the composite denominators are multiples of other rational numbers
(e.g. 
and 
). To view the interactive Java Sketchpad version of the
construction of 
, click here.
Constructible Radicals – Area Model
Rational
numbers are not the only constructible numbers. We can also construct some radicals,
including square roots of rational numbers. The construction of 
is shown below. This
length can be shown to be the using the area model
and demonstrating a square with area of two, such that the area of the orange
square is one-half the area of the whole square, or 
. A square with area 2 has sides 
.
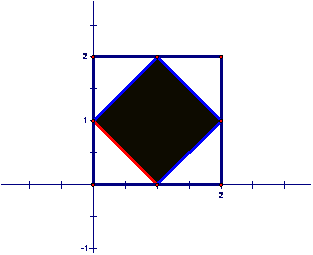
Similarly,
any constructible area leads to a constructible square root. A square of area 3
can be constructed as shown below. The area of the large square is the square
of 
, or 
. Each green triangle is 
, such that the sum of the yellow triangles is 
, making the area of the blue square 3. The red sides of this
square, therefore, represent 
. (The blue segment is the unit (1) and the magenta segment
is 
.)
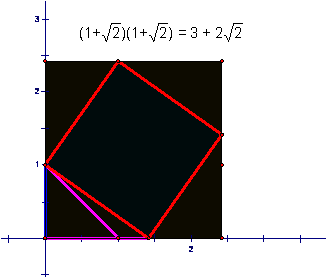
In similar
fashion, all square roots can be constructed, as can their multiples One
representation of the construction of the radicals 
through 
is shown below. Also,
imbedded radicals, such as 
can be found, provided only the radical square root is
used.
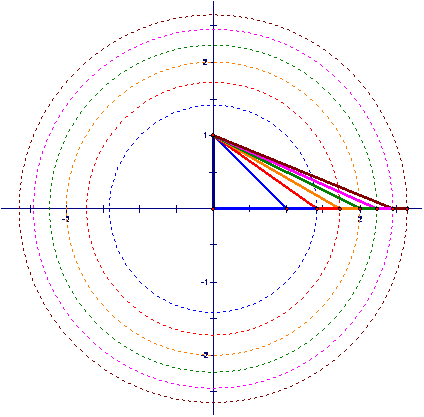
Another representation
of the construction of the radicals 
through 
is shown below. This
construction is called a square root spiral.
Be sure to investigate the above constructible lengths using the Geometer’s Sketchpad file linked here.
Constructible Angles – What angles can be constructed? (Limited to integer values, for now…)
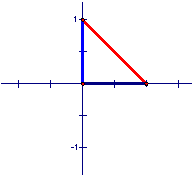
Based on the construction of perpendicular lines, a 90º angle can be constructed. Also, any multiple of a constructible angle is constructible. For simplification, consider the angles between 0º and 90º. Since angle bisectors are constructible, 45º is constructible.
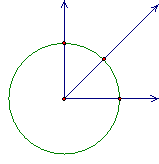
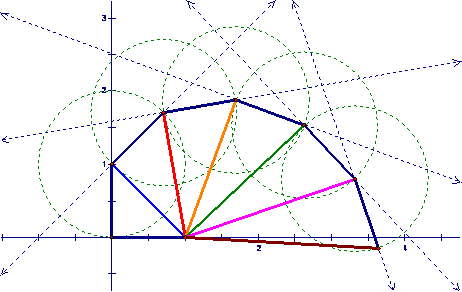
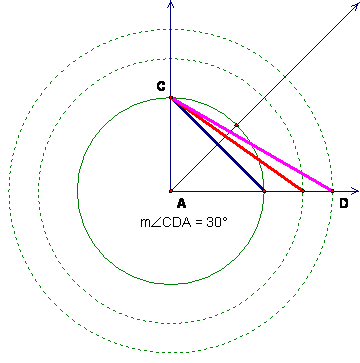
Since
the lengths 1, 2, and 
are constructible, a
30º–60º–90º triangle is constructible, as shown below. Therefore, 30º and 60º
are constructible, as is 15º, since it is one-half of 30º.
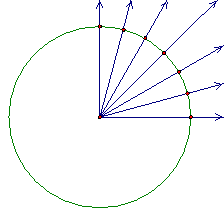
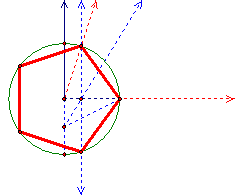
Since a pentagon is constructible, 72º is constructible, as is 36º, 18º, 9º, since these are one-half of each other. Therefore, the multiples of 9º are constructible.
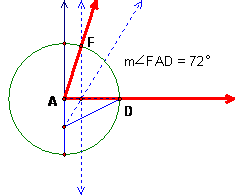
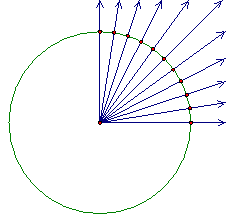
Now, because the multiples of 9º and 15º are constructible, 15º and 18º are constructible. Since angles can be added and subtracted, 3º = 18º – 15º is constructible. Finally, all multiples of 3º are constructible.
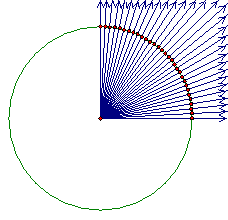
There are many more constructible angles, but not integral ones other than the further multiples of 3º. This is based on the constructible polygons.
http://en.wikipedia.org/wiki/Compass_and_straightedge
http://planetmath.org/encyclopedia/ConstructibleAnglesWithIntegerValuesInDegrees.html
http://mathworld.wolfram.com/ConstructiblePolygon.html