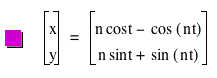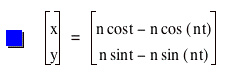Cycloids
by
Diana May
Investigation
#10 ~ A cycloid is a locus point on the rim of a
circle as the circle rolls along a straight line. So, the center of the circle moves along a path parallel to
the straight line and at a constant rate.
To
investigate the cycloid, let’s first look at the basic parametric equations for
a cycloid:
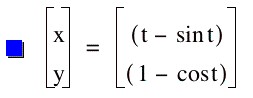
Upon graphing these equations, if
we let t range from 0 up to π, 2π and 3π, we get the following graphs:
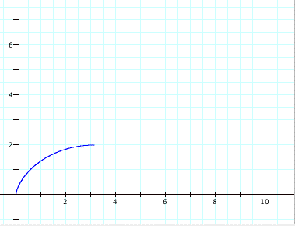
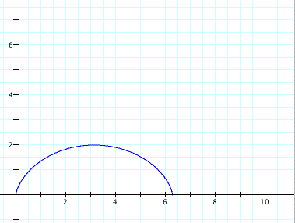
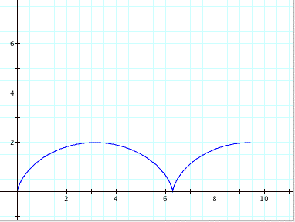
As we can see from the graphs, as
t increase by π, the path moves
along half of the complete path. A
full cycle is reached after t has cycled 2π.
Now, let’s consider what happens
if we multiply the functions by a constant:
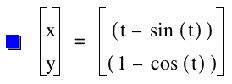
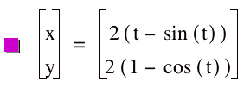
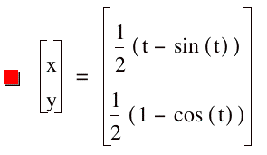
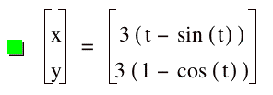
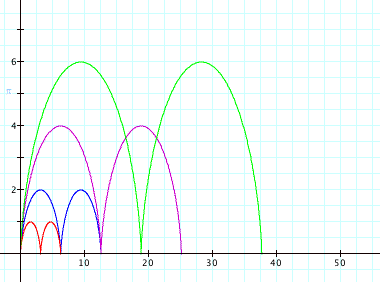
We can see that the coefficients
cause the curves to grow (or shrink), but do not affect how many cycles the
curve goes through. Also, notice
that the coefficient affects the maximum x-value reached and the maximum
y-value reached, which we’d expect in parametric equations because the
coefficient is in the y equation as well as the x equation.
By making the coefficients
negative, we can get a cycloid in any of the quadrants:
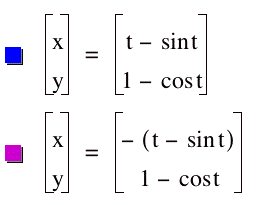
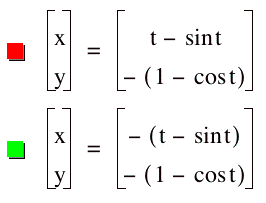
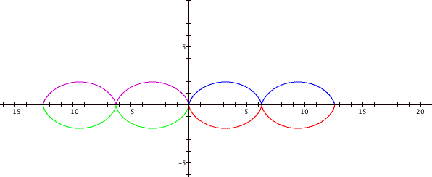
Let’s look at the mathematics
behind manipulating the constant.
First, consider the arc length of a single hump of the cycloid:
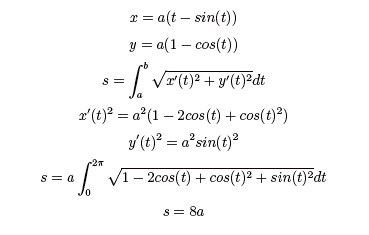
From this, we can see that the arc
length increases by 8 units for every 1 unit increase in a. We can also consider how the area under
a hump changes as a changes:
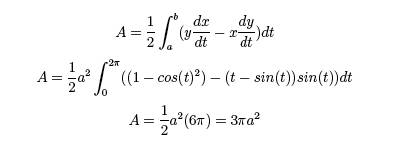
So, as a increases by a unit, the
area increases by 3π(2a + 1) units2.
The height of each hump is the
maximum y-value, which occurs at odd multiples of π. To find the height of a hump, we simply plug t = π into the
y equation:
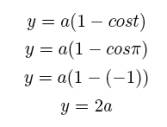
So, the height of a hump is 2 times the coefficient.
Now, let’s see how changing the coefficient on t changes the cycloid.
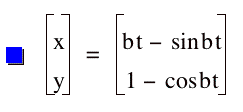
By graphing values of b at 1, 2, and 3, we get the following respective graphs:
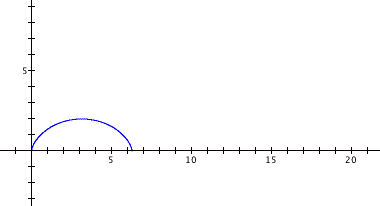
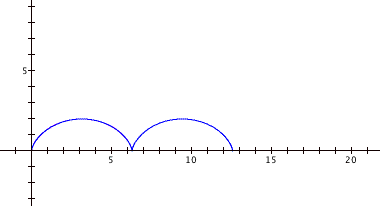
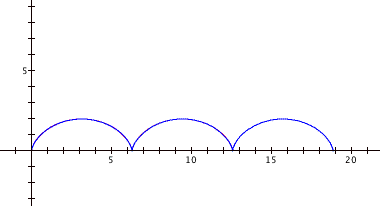
Increasing the coefficient on t only increases the number of humps of the cycloid; it does not affect the size (height or width) of the humps. Without a coefficient, letting t range from 0 to 2π gives us one hump. With a coefficient of b, t now ranges from 0 to 2πb, so we would expect b humps. To see a movie on how the coefficient changes the graph, click here.
Other types of
cycloids:
Hypocycloid: the curve produced by a fixed point on the circumference of a circle that rolls around the inside of a larger circle.
For a GSP construction of the hypocycloid, click above.
The parametric equations for a hypocycloid are
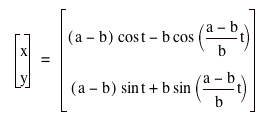
where t is the angle from the center of the large circle to that of the small circle, a is the radius of the larger circle, and b is the radius of the smaller circle.
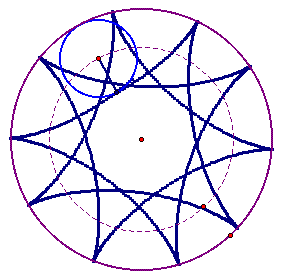
If we consider the following equations, with n = 0, …, 10, we get a range of stars with n-1 points. To see a movie on how the graph changes as n changes, click on the equations.
Epicycloid: The curve produced by a fixed point on the radius of a circle that rolls along the outside circumference of a larger circle.
For a GSP construction of an epicycloid, click above.
The parametric equations for an epicycloid are:
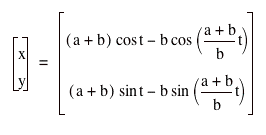
where a and b are the radii of the larger and smaller circles respectively and t is the angle from the center of the larger circle to that of the smaller circle.
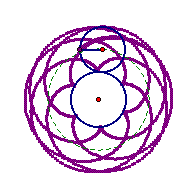
If we consider the following equations, with n = 0, …, 10, we get a range of roses with n-1 loops. To see a movie on how the graph changes as n changes, click on the equations.
Questions? E-mail me.