Linear Functions

Assignment 1 - Diana May

In this assignment, we're going to consider various arithmetical operations on linear functions.

First, we’ll consider functions with opposite slopes.

f(x) = 3x - 4 and g(x) = -x + 4

a. h(x) = f(x) + g(x)

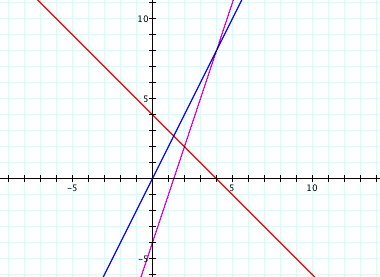
*Notice that the sum of the functions intersects the individual functions when one of the functions is at y = 0. This is because when the one function is zero, the only thing contributing to the sum is the other function, so their y-values are equal.

*Also, it appears that the sum crosses the y-axis when its y-value is equidistant from the original functions’ y-values.

*If we looked at the sum of the functions, h(x) = f(x) + g(x) = 3x - 4 + -x +4 = 2x. This is the line we see for h(x) in the graph because h(x) has a slope of 2 and a y-intercept of 0.

b. h(x) = f(x)*g(x)

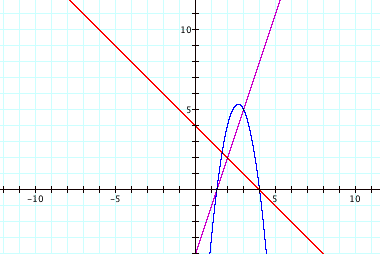
*When we multiply the two functions, we get a parabola that has its roots when one of the original equations crosses the x-axis. This is expected because h(x) = (3x-4)(-x+4), so h(x) = 0 when one of the two quantities is 0.

*The maximum of the parabola is at x = 8/3.

c. h(x) = f(x)/g(x)

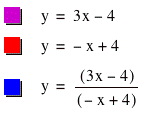
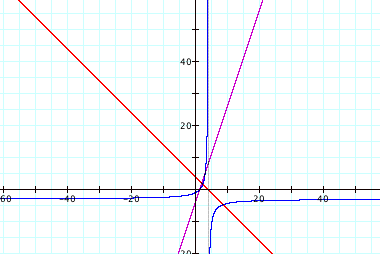
*There is a vertical asymptote at x = 4 because when x = 4, the denominator (-x+4) equals 0, making the function undefined.

*There is also a horizontal asymptote at y = -3. If we look at h(x) = (3x-4)/(-x+4) and consider what happens as x gets very large (positively and negatively), we see that we are getting values that approach the ratio of the slopes. For example, h(100) = (300-4)/(-100 + 4) = 296/-96 = 3.083. Increasing x, h(1000) = (3000-4)/(-1000 + 4) = 2996/996 = 3.008. You will never actually get 3 as a result though, because of the –4 in the numerator and the +4 in the denominator.

d. h(x) = f(g(x))

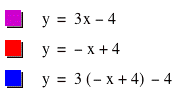
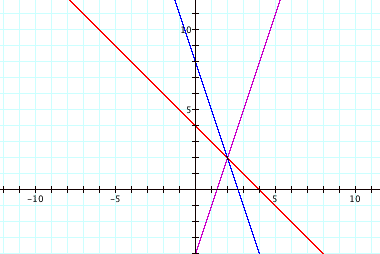
With this composition of the two functions, it appears as though the composition splits down the middle of the two original functions. In other words, at any given value of y, the x-value of the composition function is equidistant from f(x) and g(x). To demonstrate this, we need to re-write each function in terms of x:

f(x) = 3x – 4 becomes x = (y +4)/3

g(x) = -x+4 becomes x = 4-y.

h(x) = 3(-x + 4) – 4 = -3x+8 becomes x = (8-y)/3.

We want to compare the distance between h(x) and both of the original functions.

The distance between h(x) and f(x) is (y+4)/3 – (8-y)/3 = (2y-4)/3.

The distance between h(x) and g(x) is (8-y)/3 – (12-3y)/3 = (2y-4)/3.

So the distance between h(x) and f(x) is the same as the distance between h(x) and g(x), for any y value.

Now, let’s look at a different pair of linear functions to see if we see the same patterns. We’ll try functions that both have positive slopes.

f(x) = x+2 and g(x) = 3x-3.

a. h(x) = f(x) + g(x)

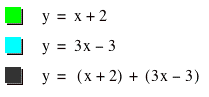
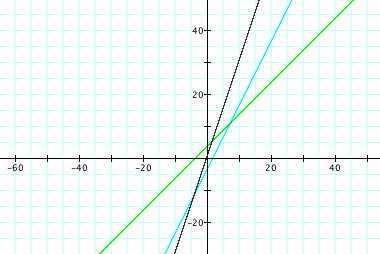
*Once again, we see that the sum of the functions intersects the individual functions when one of the original functions is equal to 0.

*Also, the sum crosses the y-axis when the y-value is equidistant from the original functions.

b. h(x) = f(x)*g(x)

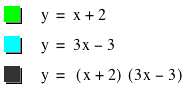
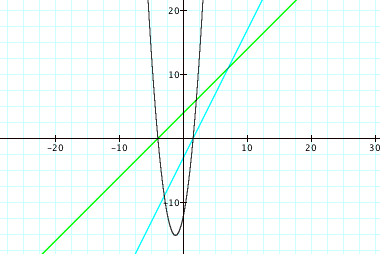
*We see that the roots of the parabola occur when one of the original functions is at 0, which is what we expected.

*The minimum occurs at x = -1/2

c. h(x) = f(x)/g(x)

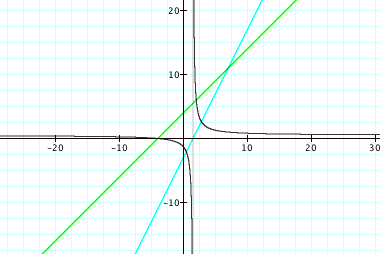
*Again, there is a vertical asymptote when the denominator of the function is zero. In this case, the denominator is 3x – 3, so the vertical asymptote is at x = 1.

*The horizontal asymptote is at y = 1/3, which is the ratio of the coefficients.

d. h(x) = f(g(x))

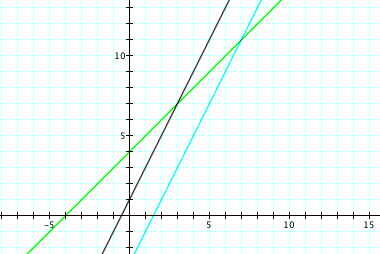
*Here, we do not have the composition splitting the original functions down the middle. Instead, the composition is parallel to one of the original functions because the other original function has a coefficent of 1 for x.

What happens to our observations if the linear functions have the same slope?

f(x) = x – 5 and g(x) = x – 2

a. h(x) = f(x) + g(x)

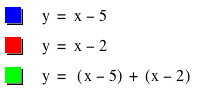
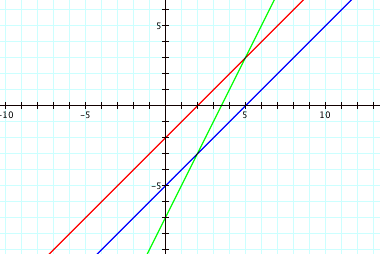
Once again, the sum crosses the original functions when the other function is at y = 0. Also, the sum crosses the x-axis when it’s x-value is equidistant from the x-values of the original functions.

b. h(x) = f(x)*g(x)

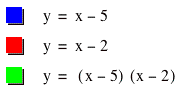
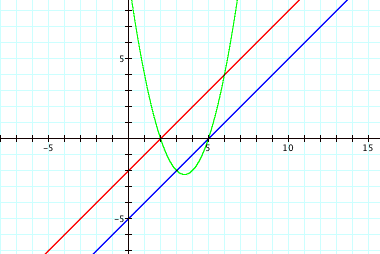
*Once again, we see the roots of the parabola occur when one of the two original functions crosses the x-axis.

*The minimum occurs at x = 7/2.

c. h(x) = f(x)/g(x)

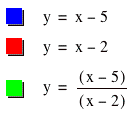
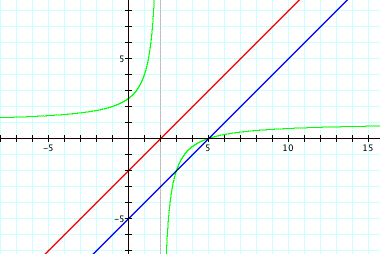
*The vertical asymptote is at x = 2 (the denominator is x – 2).

*The horizontal asymptote is at y = 1 (the ratio of the slopes is 1:1).

d. h(x) = f(g(x))

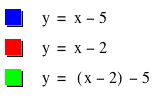
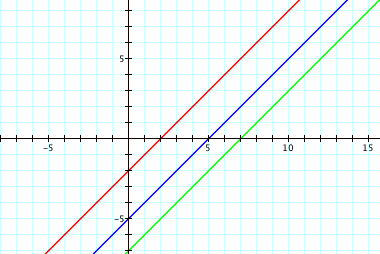
*Here, h(x) = (x – 2) – 5 = x – 7. In this case, the composition never falls between the two lines. It is parallel to both of them and has a y-intercept that is the sum of the original functions’ y-intercepts.

To see a movie on how modifying one of the functions affects h(x), click below:

Questions? E-mail me.

Return.