
Quadratic Equations
Assignment 3 - Diana May
Investigation
#2 ~ Let’s consider the effect the coefficients a, b, and c have
on the roots of the quadratic equation.
First,
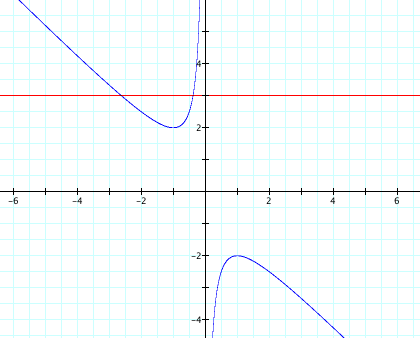
we’ll graph x2 + bx + 1 =0 in the b-x plane. Notice that any point on the curve
corresponds to a root at that x-value when the quadratic has that b-value. We have drawn in the line b = 3, which
shows that y = x2 + 3x + 1 has 2 roots, one at x ≈ -2.618 and the
other at x ≈ -0.382.
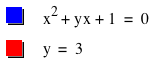
Let’s see what
happens if we vary the c-value:
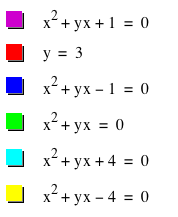
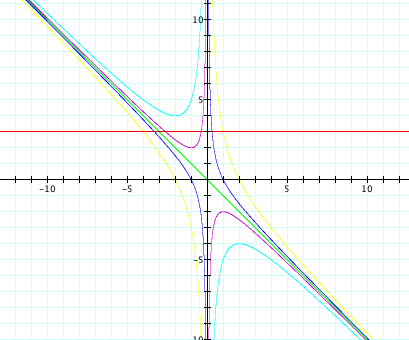
Notice that when c = 0, there is exactly one root and we get a
straight line of b = -x, which we’d expect because x2 + bx = 0 is
the same as b+x = 0. Also, when c
< 0, there are two real roots for the quadratic, but if c > 0, the number
of roots varies depending on b.
From the
quadratic formula, we know that for real roots to exist for the quadratic
equation, b2 – 4ac must be greater than or equal to 0. Otherwise, we would not be able to take
the square root of that quantity.
So, it must be the case that b2 ≥ 4ac. Since, in our case, a = 1, if c is
negative, this will always hold.
However, if c is positive, then b ≥ 2c1/2. To see a demonstration of when the
quadratic equation has exactly one real root, we graph the equations x2
+ bx + n = 0 and b = 2n1/2.
The red line shows the positive square root. Click HERE
for the movie.
Investigation
#3 ~ Now, let’s
consider the equation 2x + b = 0:
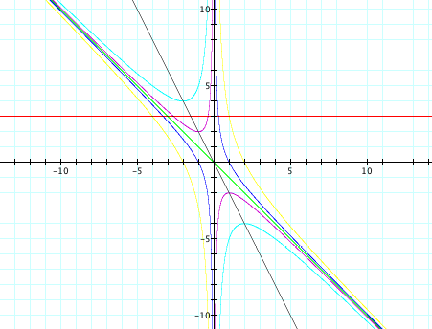
What does the addition of
this equation to our graph tell us?
From the quadratic formula, we know that the minimum (or maximum) of the
parabola is located at x = -b/2a.
In this case, a = 1, so the minimum is at x = -b/2, which is equivalent
to 2x + b = 0.
The black line in
our graph tells us that the minimum will be located at that x-value, given a
quadratic equation with that b-value.
Investigation
#4 ~ Let’s consider the
effect the c constant has on the parabola by examining graphs in the xc-plane:
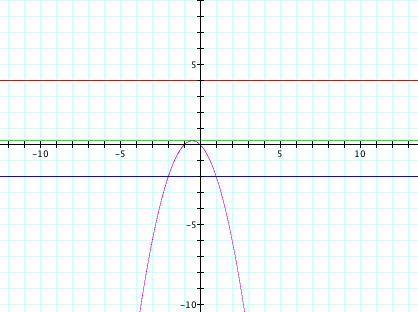
The green line
represents when there is exactly one root (which, from the quadratic formula is
when b2 = 4ac). The
blue line shows that for c values below 1/4, the equation has two roots. From
the red line, we see that for c values that are above 1/4, the equation has no
roots.
Questions? E-mail me.