
Equal
Distances
Assignment 6 - Diana
May
The problem: Locate the point X on AC and Y on CB such that
XA = YB = XY.
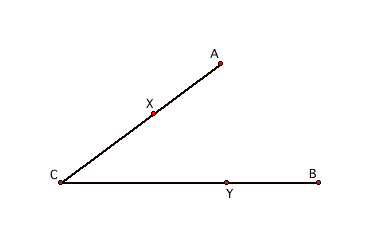
First, let’s construct the segment AB and choose a random point on CB:
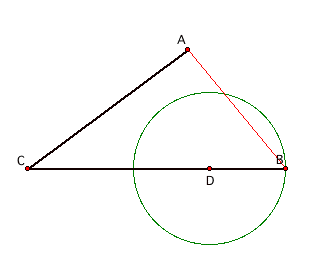
Now, let’s draw a line through D, that is parallel to AC. We’ll label the intersection of the
parallel line and the circle E.
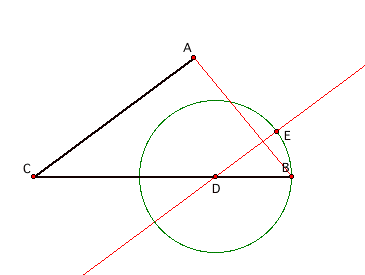
Let’s construct another circle with radius DE, but centered at E. Notice that DE and DB are equal because
they are both radii of the same circle.
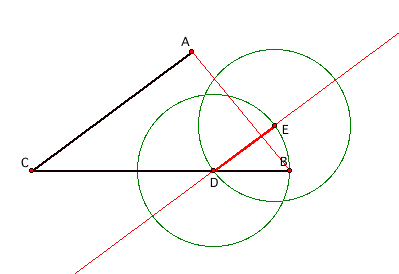
We’ll label the intersection of our new circle with AB as the point
F. Let’s construct a line parallel
to DE that goes through the point F.
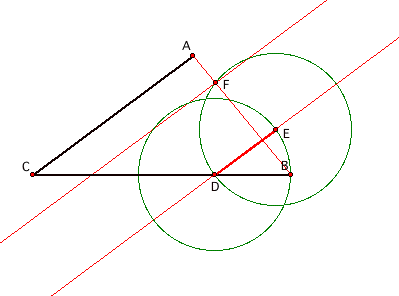
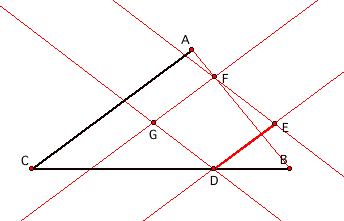
Construct a line through EF and another line parallel to EF through
D. Hide the circles to make
the drawing less cluttered.
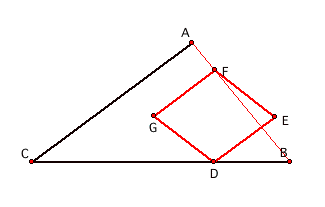
Notice that EF and DG are equal because they were constructed by parallel lines. Similarly, DE and FG are equal. From before, we know that DE and EF are equal, so the figure below is a rhombus.
Construct a line through BG and label its intersection with AC as
X. Construct a line parallel to GD
that runs through X. Label its
intersection with BC as Y.
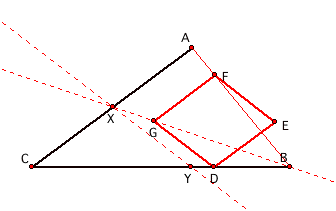
How do we know that X and Y are the points we are looking for? From similar triangles:
Triangle GDB is similar to triangle XYB. Also, triangle GDB is an equilateral triangle because GD =
DB. Therefore, triangle XYB is
also an equilateral triangle and XY = YB.
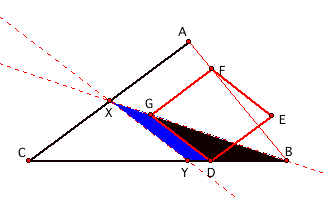
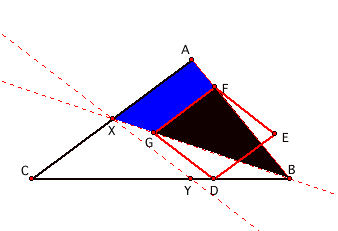
Also, triangle BGF is similar to triangle BXA. Since GD = DB = GF, we have that XY =
YB = AX.
Questions? E-mail
me.