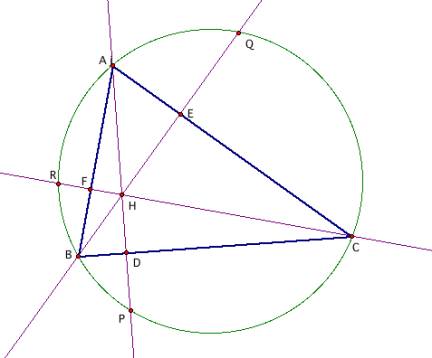
Altitudes
Assignment 8 -
Diana May
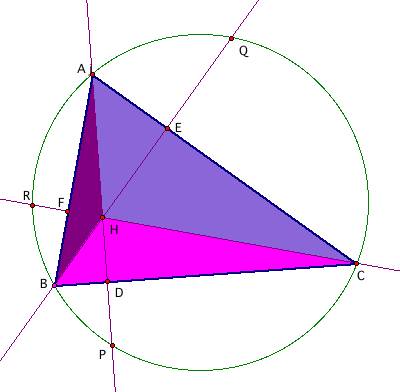
Construct
any acute triangle ABC and its circumcircle. Construct the three altitudes AD, BE, and CF. Extend each altitude to its
intersection with the circumcircle at corresponding points P, Q, and R. For a GSP sketch to explore with this
construction, click below:
Claim:
The ratios AP/AD, BQ/BE, and CR/CF sum to 4.
Proof:
First, let’s consider how we can break the
segments into ratios:
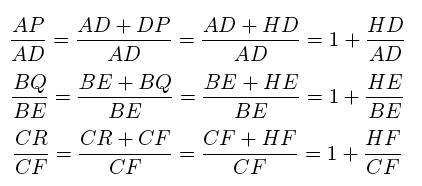
With these ratios, we can see that all we have
to show is that HD/AD +HE/BE + HF/CF = 1:
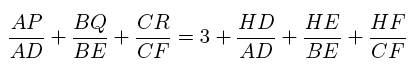
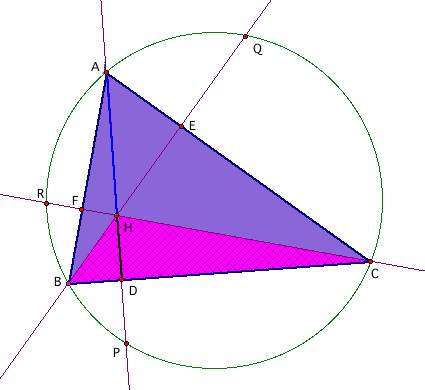
Let’s consider the first ratio, HD/AD. HD is the altitude of the triangle BHC
and AD is the altitude of the triangle ABC, so we can use them in the formula
for the areas of the triangles BHC and ABC:
So, we have that:
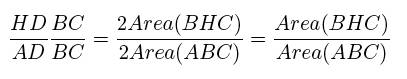
We can consider a similar argument regarding the
remaining two ratios:

When we plug our areas into our original
equation, we get:
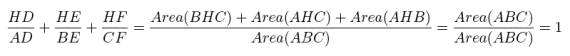
Notice that Area(BHC)+Area(AHC)+Area(AHB) = Area(ABC)
because those three triangles make up the triangle ABC:
Now that we know that HD/AD+HE/BE+HF/CF = 1, we
get our conclusion:
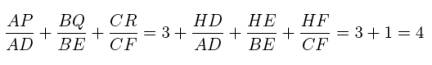
Questions? E-mail
me.