Pedal Triangles
Assignment 9 Ð Diana May
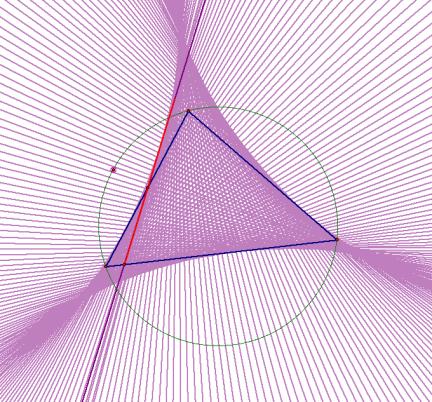
A pedal triangle is constructed
as follows:
*Construct triangle ABC and
extend the segments.
*Pick any point P in the plane.
*Construct perpendicular lines
between each segment of the triangle ABC and point P.
*The triangle formed by the
intersections RST is the pedal triangle corresponding to the point P.
To
open a GSP file with a script tool for constructing pedal triangles, click HERE.
Is there anything interesting you
notice when you pick specific locations for P?
One thing that can be seen is
that certain locations of the point P cause the pedal triangle to collapse onto
a line. This line is known as the Simson
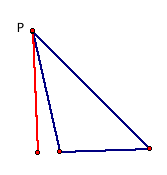
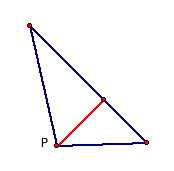
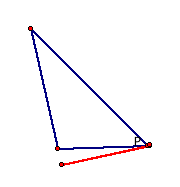
line. Where exactly are all of these points located? First, observe that if the pedal point
is located at any one of the vertices, the pedal triangle is degenerate:
With a
little bit of trial and error, it seems that the collection of points that
cause the pedal triangle to collapse to a line seems to form a circle that
contains the triangle vertices. In
fact, if the point P is anywhere on the circumcircle, we get a degenerate pedal
triangle.
Claim: The pedal triangle of a triangle ABC is degenerate if and
only if P lies on the circumcircle of triangle ABC.
Proof:
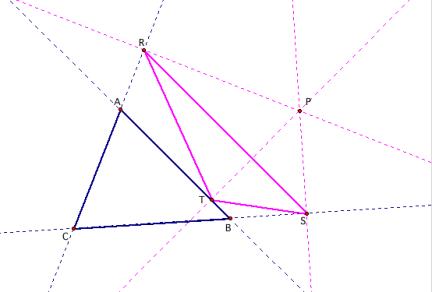
Let P be on the circumcircle of the triangle ABC. Without loss of generality, let P be on the arc AC that does not contain B. Notice that the angles PCÕA, PBÕC, and PAÕC all are right angles:
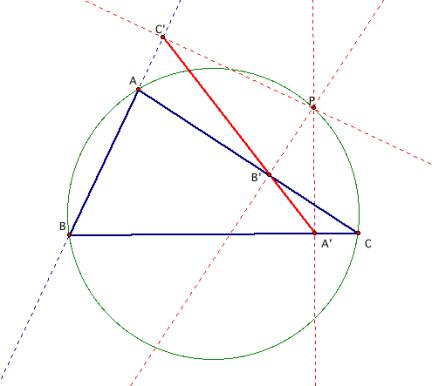
Because those angles are right angles, P also lies on the circumcircles of the triangles AÕBCÕ, AÕBÕC, and ABÕCÕ.
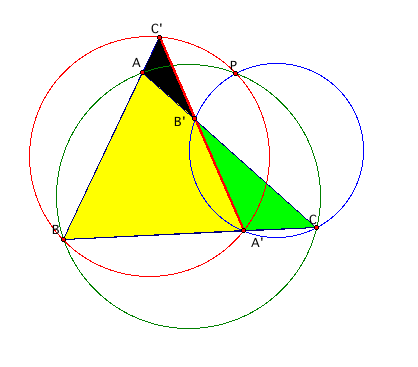
Therefore,
we have that the angle APC = 180o Ð angle ABC = angle CÕPAÕ. If we subtract the angle APAÕ from
angles APC and CÕPAÕ, we are left with angle AÕPC = angle CÕPA.
Because
AÕ, P, C, BÕ lie on a circle, we have that angle AÕPC = angle AÕBÕC.
Similarly,
since A, BÕ, P, CÕ lie on a circle, we have that angle CÕPA = angle CÕBÕA.
From
transitivity, we have that angle AÕBÕC = angle CÕBÕA. Therefore, AÕ, BÕ, CÕ are collinear (angles AÕBÕC and CÕBÕA
are vertex angles).
Now,
suppose that the points AÕ, BÕ, and CÕ are collinear. Does that mean that P lies on the circumcircle?
Without
loss of generality, we can assume that P is situated on the inside of the angle
ABC on the opposite side of AC.
Also, we can assume that CÕ lies on the line AB past A.
Reversing
the argument from the previous proof, we have that the angle APC = 180o
Ð the angle ABC, so P lies on the circumcircle.
The collection of Simson lines as P travels around the
circumcircle
Questions? E-mail me.