
Bouncing Barney
Final
Project – 2A - Diana May
Barney is in the triangular room
shown here. He walks from a point on BC parallel to AC. When he reaches AB, he
turns and walks parallel to BC. When he reaches AC, he turns and walks parallel
to AB. Prove that Barney will eventually return to his starting point. How many
times will Barney reach a wall before returning to his starting point?
To investigate this problem, let’s
first try it by picking a general point P on BC and follow the directions
above:
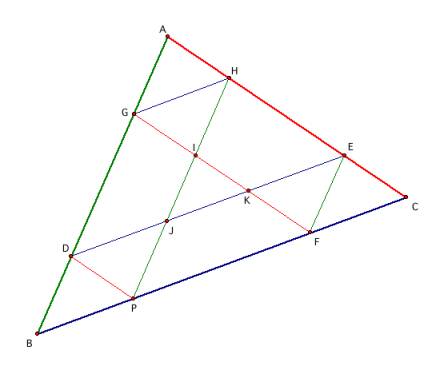
From this attempt, Barney returns to
his starting point P after 5 bounces (return to starting point is the sixth
wall).
Is it possible to find a location
where the number of bounces is greater than 5?
Let’s assume there is a starting
point X on BC that results in more than 5 bounces to return to the starting
point. Clearly, X is not equal to
P.
Because lines AB, HP, and EF are
parallel and lines BC, DE, and GH are parallel, we have that angles ABC, ADE,
AGH, HJE, HPC, and EFC are congruent.
Similarly, since lines AB, HP, and
EF are parallel and lines DP, GF, and AC are parallel, we have that angles BDP,
BGF, BAC, PIF, PHC, and FEC are congruent.
Also, since lines BC, DE, and GH are
parallel and lines DP, GF, and AC are parallel, we have that angles DPB, GFB,
GKD, AHG, AED, and ACB are congruent.
From
those congruent angles, we have that the following triangles are similar: ABC,
ADE, HJE, HPC, AGH, EFC, and DBP.
When two
triangles are similar, we know that the ratios of their sides are equal. Therefore, BP/BC = FC/BC.
But,
none of the above is specific to our point P, so it must also hold for X. Therefore, BX/BC = FC/BC which implies
that BX = FC.
Consider
the triangles BDP and FGC. We
already know that the corresponding angles of these triangles are
congruent. Also, we know that CEDP
and BDEF are parallelograms.
Therefore, CE = DP and BD = FE.
So, triangles BDP and FEC must be congruent and BP = FC. But, BX = FC, therefore it must be that
P = X. This contradicts our
original statement and therefore there must not be a location on BC that will
give you more than 5 bounces before returning to the starting point.
To investigate
with a GSP sketch of the Bouncing Barney problem, click HERE. Notice that it is possible for Barney
to return to his starting point after only 2 bounces. Where does P have to be located for that to occur? What happens if P is located at a
vertex?
Now, let’s
consider what would happen if we were to let Barney start outside of the
room. Would he still return to his
starting point after 5 bounces? To
explore this idea with GSP, click HERE.
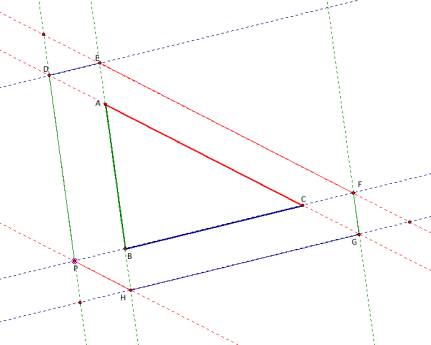
It
appears that Barney will return to his starting point after 5 bounces.
If we
assume there is an X on the line BC beyond B that is not P, a similar proof to
the one given above shows that triangles PHB and CGF are congruent and PH =
CG. Therefore, CF = PB and that
would hold for any point P, so X = P.
Questions? E-mail me.