Ceva’s Theorem
Final Project – 2B -
Diana May
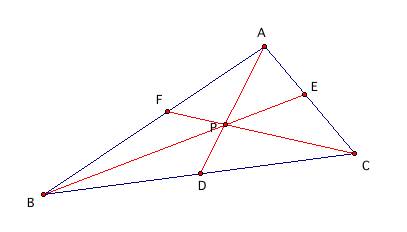
Given a triangle ABC, pick a random point P inside the triangle. Now, draw a line from each vertex, through P, and extend to the opposite side. Looking at the measurements of the parts of the sides, what do you notice about the products (AF)(BD)(CE) and (BF)(CD)(AE).
For a
GSP file to try different locations for P and observe how the measurements
change, click below:
So, it seems that no matter where P is located:
(AF)(BD)(CE) = (BF)(CD)(AE).
Can we prove this?
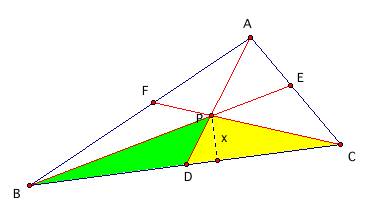
First, notice that triangles BPD and CPD have a common altitude, x. So, Area(BPD) = (BD)x/2 and Area(CPD) = (CD)x/2.
So, BD/CD = Area(BPD)/Area(CPD).
|
|
|
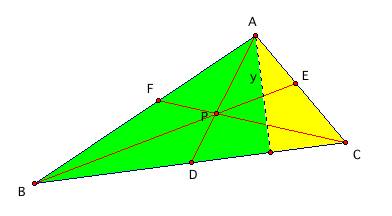
Now, look at
triangles ABD and ACD:
We get common
altitude, y, which gives us
Area(ABD) = (BD)y/2 and Area(ACD)
= (CD)y/2.
So, BD/CD =
Area(ABD)/Area(ACD).
From the two
equations for BD/CD, we get:
BD/CD = Area(APB)/Area(APC)
If we had started
with the other two sides instead of BC, we would have gottten the following:
CE/AE =
Area(CPB)/Area(APB)
AF/BF = Area(APC)/Area(CPB)
|
|
|
Now, when we
multiply our results, we get:
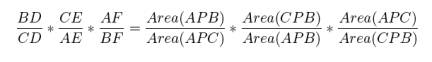
Since the areas in the
numerators and denominators cancel out, we see that the ratio is simply equal
to 1. Therefore, (BD)(CD)(AF) =
(CD)(AE)(BF).
Now, what if we were
to allow P to be outside of the triangle?
For a GSP sketch,
click HERE.
It seems that our
property holds even if P is outside of the circle.
Questions? E-mail
me.