By

Ronnachai Panapoi

In this assignment, we will talk about the parametric equation, particularly, the parametric equation of a line.

Let’s review about the parametric curve.

The parametric curve in the plane is a pair of functions,

x = f(t)

y = g(t), where the two continuous functions define ordered pairs (x, y).

The two equations are usually called the parametric equations of a curve.

The extent of the curve will depend on the range of t.

I will start with these following parametric equations of a straight line,

x = a + t

y = b + kt

We next will investigate the graphs of these equation for selected values of a, b, and k in an appropriate range for t.

Click HERE to see and explore in this file.

Firstly, I restrict the range of t between -5 and 5. (We can change this range of t, but it does not affect to the graph in these cases.)

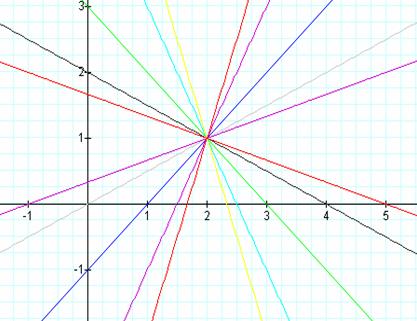
In this exploration, I have fixed the values of a and b as 2 and 1, respectively, then I observe the graphs with the value of k varies.

In these cases, the graphs have the point in common which is (2, 1).

Also, I can notice that the value of k affects to the direction of the line segments. In other words, if k is positive, the line segment goes up left to right. By contrast, it goes down from left to right if k is negative.

These observations of k give us the result similar to the slope of the line.

We then investigate the effect of line segments from changing the value of a and b.

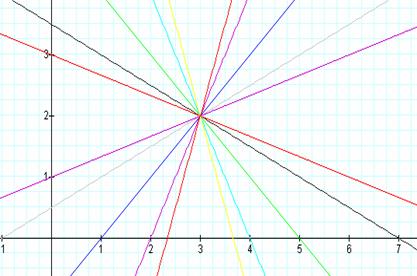
These graphs have the new common point as (3, 2) when the value of a and b are changed to be 3 and 2 respectively.

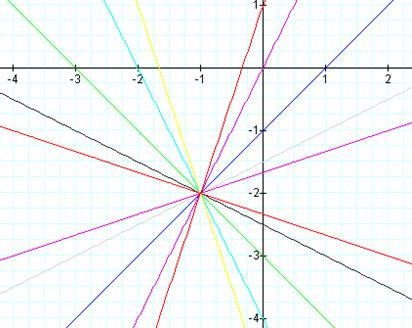
These graphs have the new common point as (-1, -2) when the value of a and b are changed to be -1 and -2, respectively.

I will verify these facts by looking back to the parametric equations.

From these parametric equations,

x = a + t

y = b + kt,

we know that x and y have the same value of t.

Therefore, we get

t = x - a and t = .

So, x - a = .

Finally, we obtain

kx – ak – y + b = 0 or kx – y + ( b - ak) = 0.

This is the equation determining the straight line.

From this equation, we get the result that the slope of this straight is = k, and the y-intercept is (0, b - ak).

In the any two cases that the values of k varies as and but a and b are fixed.

Hence, we have the two equations resulting from these events as follows.

-----------(*)

and -----------(**)

We then can solve for the intersection point of these two equations.

From (*), we get

------------(***)

Substitute (***) in (**), we have

x = a

So, y = b

Thus, the intersection point of these two equation when k varies and a and b are fixed is (a, b).

These verifications correspond to the previous observations.

Now, let’s use the previous proof to make some conclusion from the following parametric equations,

x = t + 1

y = 2t – 1,

for some appropriate range for t.

Compare these equations to the previous ones,

x = a + t and y = b + kt,

We have a = 1, b = -1, and k = 2

Think of the facts from the previous proof, we know that these parametric equations are of the straight line determined by the equation,

2x – y + ((-1) – (1)(2)) = 0

2x – y – 3 = 0

Click HERE to see whether our assumption is correct.

Lastly, how can we write the parametric equations of a line segment through (7, 5) with slope of 3?

The straight line passing through (7, 5) with slope of 3 is determined by the equation,

y – 5 = 3(x - 7) or 3x – y – 16 = 0.

Then, we have 3x – 16 = y

Let x = t,

so y = 3t – 16.

We therefore get the parametric equations of the straight line passing through (7, 5) with the slope of 3 as

x = t

y = 3t – 16, where

Click HERE to see in the gcf file.

RETURN