
By
Ronnachai
Panapoi
![]()
In
this assignment, we will investigate the way to construct the circle tangent to
the two circles with one point of tangency being the designated point.
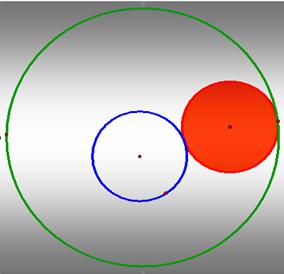
In
this figure the red circle is tangent to the other two circles, the green one
and the blue one.
While we investigated, we would see
that there are three possible ways:
1. The smaller
circle lies inside the bigger one.
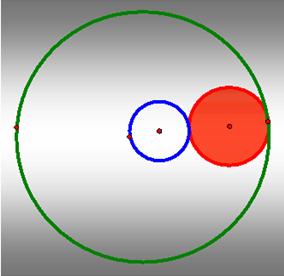
In
this case, the tangent circle also lies between the larger and the smaller
circle and it is inside the bigger circle.
2. The smaller circle lies outside the bigger one.
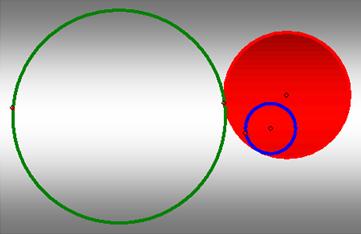
In
this case, the tangent circle lies outside the bigger circle whereas the
smaller circle lies inside the tangent circle.
For
these two cases, we can construct the tangent circle as follows:
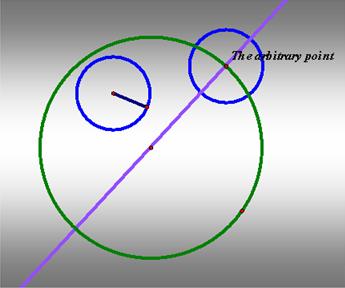
1. We first choose the arbitrary point on
the larger circle. Since we know that at the point of tangency must lie on the
diameter of the larger circle, we then draw the line passing through the center
of the circle and the arbitrary point. This is because at the tangent point,
the radius of the bigger circle must be perpendicular to the tangent line.
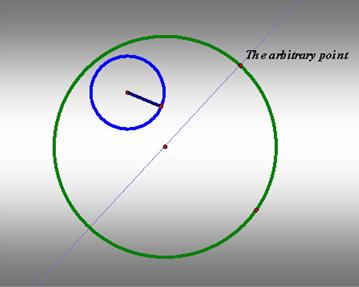
2. Construct the circle center at the
arbitrary point with radius equal to the smaller circle.
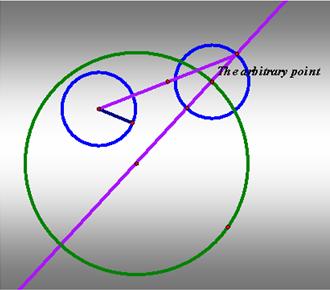
3. Draw the segment from the center of the
smaller circle to the tangent point. Then, construct the midpoint.
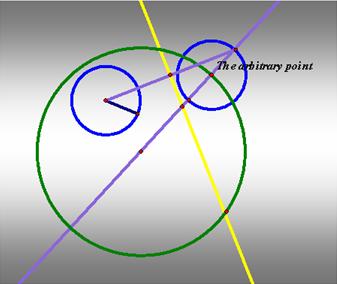
4. Construct the perpendicular line through
the midpoint. The intersection of the perpendicular and the line going through
the larger circle’s center and the tangent point is the center of the tangent
circle which we want.
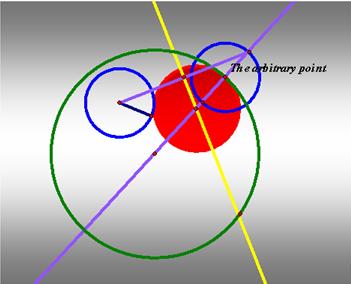
Like
the above construction, if the smaller circle is external the larger circle,
the larger or the smaller circle is inside the tangent circle.
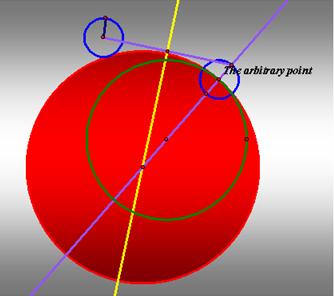
The first
case shows the larger circle is internal the tangent circle.
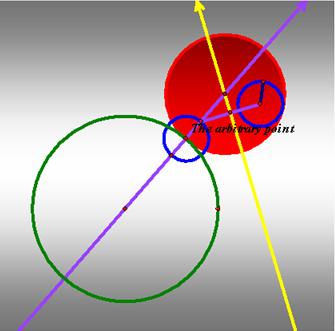
The
second case shows the smaller circle is internal the tangent circle.
However,
there is another case that the smaller circle is
inside the tangent circle and both of them lies in the bigger circle.
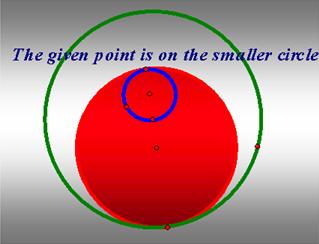
Click HERE
to explore when this case occurs.
We
will be able to observe that the centers of these three circles are collinear.
This is a key to construct to create a tool for this case.
The
construction is similar the previous construction. However, instead of drawing
the segment from the center of the smaller circle to the tangent point, we
construct the segment between the smaller circle’s center and the intersection
point of the circle center at arbitrary and the radius of the bigger circle.
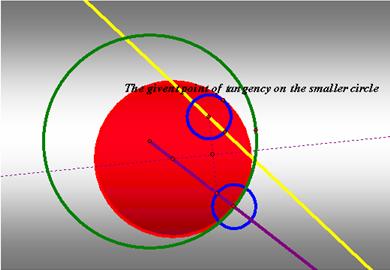
Click HERE
to see the script tool.
From the possible ways we mentioned
previously, we now will explore some facts getting from tracing the center of
the tangent circle whereas the point of tangency is moving around the larger circle.
First, the case that the tangent circle and the smaller
circle are internal the larger circle.
The
yellow trace of the center of the tangent circle is the locus of the ellipse.
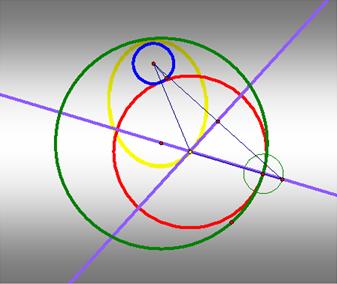
Click HERE to see the trace in GSP file.
Second, the
smaller circle is outside the larger and the larger circle is internal the
tangent circle.
The
yellow trace of the center of the tangent circle is the locus of the hyperbola.
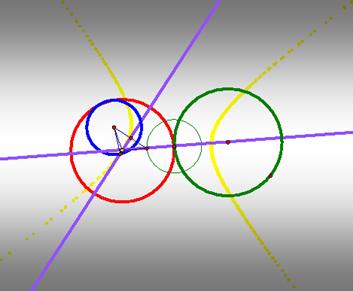
Click HERE to see the trace in GSP file.
Third, the smaller circle and the tangent circle are internal
the larger circle.
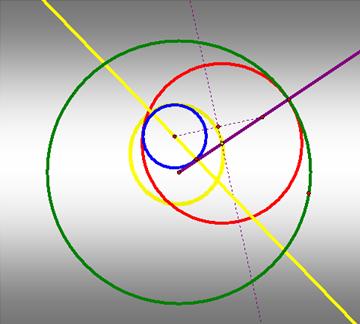
Click HERE
to see the trace in GSP file.
How does each step make sense and why is the trace the locus
of ellipse or hyperbola?
I
think this is the important part that teachers should emphasize rather than
only let the students remember the steps of construction.
