By
Ronnachai Panapoi
We will discuss on some interesting
topic in Geometry, the pedal triangles. I will start with introducing the pedal
triangles and I then choose some problem to investigate. After investigating, I
will show the proof which I got.
At
the beginning, let me give the some information of what is the pedal triangle.
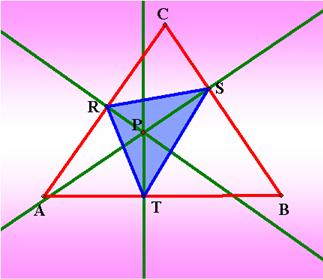
Let the triangle ABC be any triangle. Then if P is any point
in the plane, then the triangle formed by constructing perpendiculars of the sides
of ABC (extended if necessary) locate three points R, S, and T that are the
intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
Click HERE
to see this figure in GSP file.
Click HERE
to see the script tool in GSP file and investigate when P is any point in the
plane of ABC.
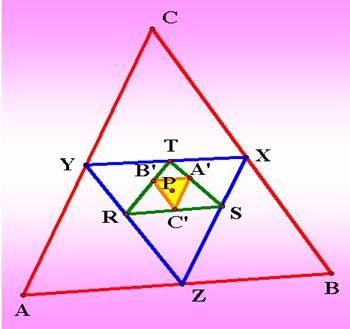
Next,
we will explore some interesting fact about the pedal triangle of the pedal
triangle of the pedal triangle of a point.
Click HERE to investigate some facts by using
GSP as a tool.
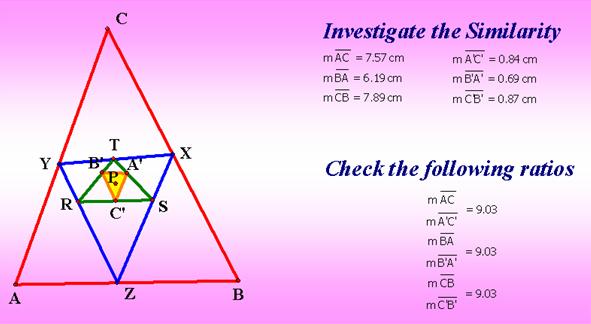
According
to the result from investigation, we will see that the pedal triangle 
of pedal triangle
RST of the pedal triangle XYZ of the pedal point P is similar to the triangle
ABC.
Now,
we will prove this fact.
Let’s
consider in the triangle and the
triangle RST.
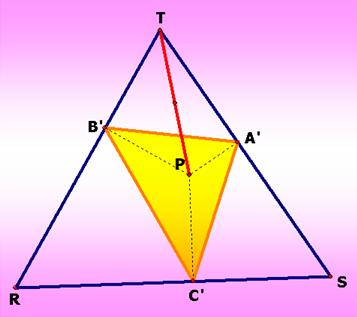
If
we draw segments from the point P to points 
, 
, and 
. We can notice that the angle PT and PT are right angles. These suggest that P lies on the circumcircle with diameter PT of the triangle T.
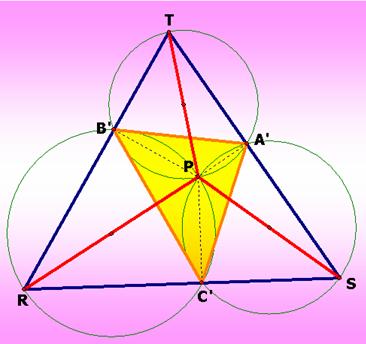
Likewise,
P also lies on the circumcircle with diameter PS of
the triangle 
and on the circumcircle with diameter PR of the triangle 
.
We
obtain
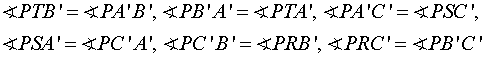
We
can look at the below figure which represents these facts.
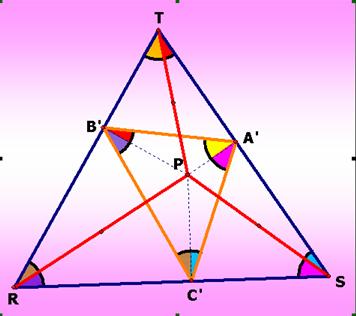
We
then consider at the triangle RST and XYZ. Similarly, we get P lies on the circumcircle of the triangles RSZ, RTY, and STX with
diameter PZ, PY, and PX, respectively.
Therefore,
we now have
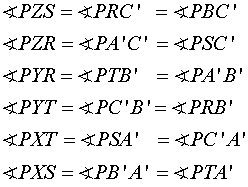
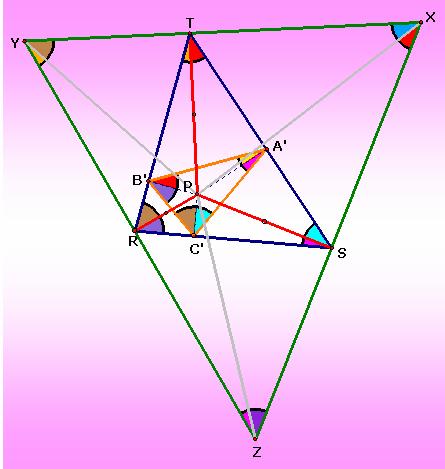
Repeat
with the same procedure, when looking at the triangles XYZ and ABC, we are able
to observe from the circumcircle of the triangle YZA,
XYC, and XZB with the diameter PA, PC, and PB, respectively and we get that
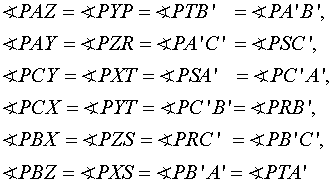
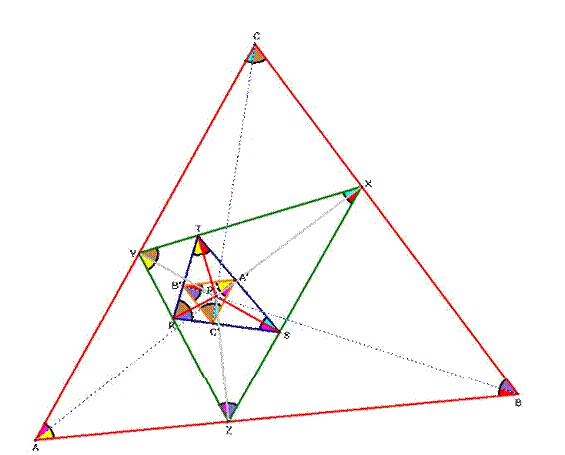
The figure above clearly shows the
facts we get.
Therefore,
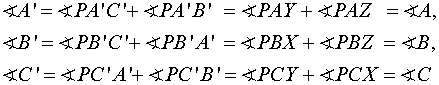
These
represent that we have completely proved that the pedal triangle of pedal triangle
RST of the pedal triangle XYZ of the pedal point P is similar to the triangle
ABC.