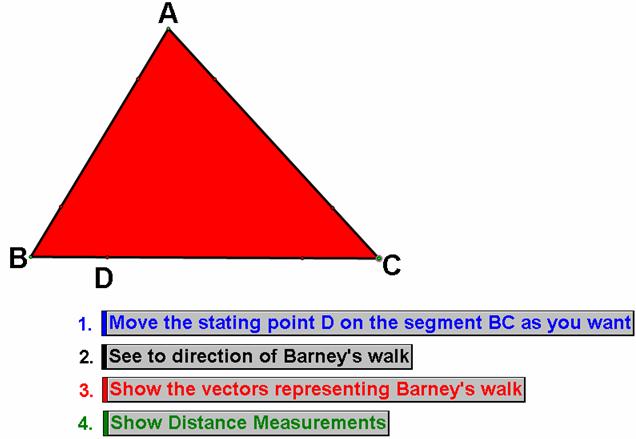
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on the line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

Let’s start exploring in the GSP before making the conclusion and verifying the mathematical conjectures with the proof.

The picture below is in the GSP file.

You can click HERE to see the investigation in GSP file.

Prior to the conjectures, let’s review some basic knowledge of a parallelogram that is needed for our proof.

“A parallelogram is a four sided figure (Quadrilateral) with two pairs of opposite sides, each pair being given by parallel line segments of equal length.”

Also, we get the fact resulted from the above definition is that the sides of a quadrilateral have opposite sides equal of equal length when and only when opposite sides are parallel.

Having explored this problem in the GSP, we obtain the following conjectures.

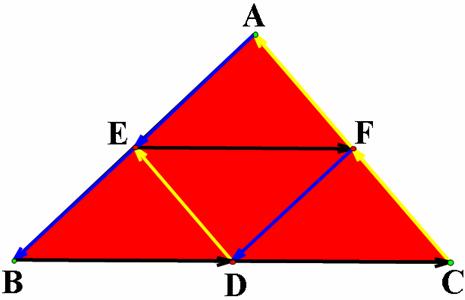
Barney will return to his starting point D after he has reached the wall for 5 times regardless of the starting point.

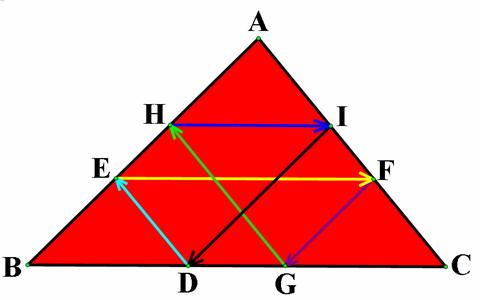
From the starting point D, Barney walks parallel to the line AC until he reaches the wall AB at point E. Then he walks from point E parallel to the line BC until he reaches the wall AC at point F. After that, he walks from point F parallel to the line AB until he reaches the wall BC again at point G.

Now, there are two possible way. One is D and G are the same. The other one is D and G are different.

If points D and G are the same, then

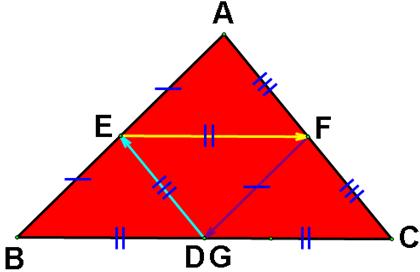
we have the triangles GBE, EFD and CDF are congruent by the SSS congruence.

Moreover, they are congruent to the triangle FEA.

In this case, we also have that the point D is the midpoint of BC.

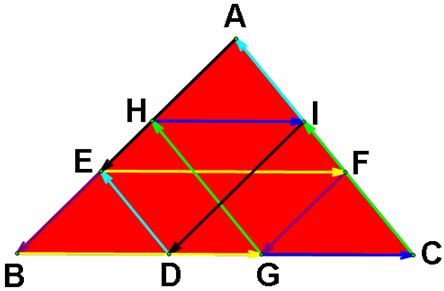
If D and G are different, he still continues walking until he reaches the point H, I, and J lying on the segments AB, AC, and BC respectively such that J is the point different from D.

The figures below represent the Barney’s walk in each he reaches the segment BC.

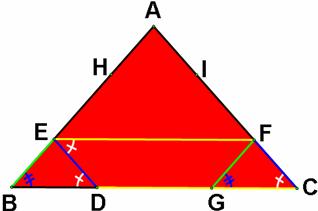
Looking at the last figure, we have HI = BJ = GC.

Due to the fact that the alternate angle of the parallel line are equal, the triangles BED and GFC are congruent by AAS congruence. We therefore get BD = GC.

Then, we have BJ = BD. This suggests that J and D are the same points.

Concurrently, we can conclude that Barney have reached the wall five times at points E, F, G, H, and I, regardless of the initial point D.

All of distances he walks inside the triangular room (from the starting point to this point again) is equal

the perimeter of the room in case that the initial point is not the midpoint of BC. In particular, if the starting point is the midpoint of BC, we have all the distance inside is a half of the perimeter of the room.

From the way that Barney walks and the previous proof, we have the direction of Barney’s walk and the parallelograms which result from his walk as below.

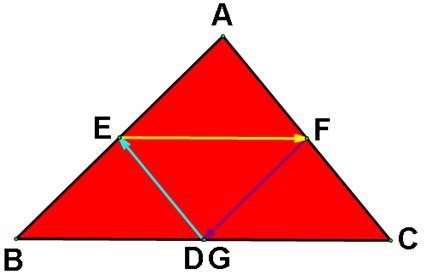
If the starting point D is the midpoint of BC, as the previous proof we get the fact that we will reaches the wall two times at points E and F, then return to the initial point D. We can see from the following picture.

Since D is the midpoint of BC, we have BD = DC

In the parallelogram EBDF, EB = FD and BD = EF, then EF = DC.

In the parallelogram EFDC, EF = DC and DE = CF.

Also, we have AE = FD and DE = FA in the parallelogram AEDF.

Since the perimeter of the triangular room is AB +BC + CA,

Therefore, it equals AE + EB + BD + DC + CF + FA = FD + FD + EF + EF + DE + DE

= 2(DE + EF + FD)

= 2(the distance of Barney’s walk inside the triangular room)

So, if the starting point is the midpoint of BC, then all the distance of Barney’s walk is a half of the perimeter of the room.

In case that D is not the midpoint of BC, from the proof in the prior conjecture we have known that his walk results in the parallelograms as shown in the following figure.

In the parallelogram DEAI, DE = IA and AE = ID.

In the parallelogram BEFG, EB = FG and BG = EF.

In the parallelogram GHIC, GH = CI and GC = HI.

Since the perimeter of the room is AB + BC + CA.

It is equal to AE + EB + BG + GC + CI + IA = ID + FG + EF + HI + GH + DE

= DE + EF + FG + GH + HI + ID = the distance of Barney’s walk.

Thus, all of distances he walks inside the triangular room (from the starting point to this point again) is equal to the perimeter of the room in case that the initial point is not the midpoint of BC.

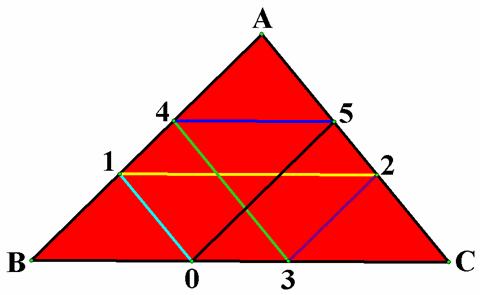
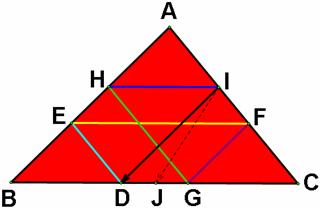
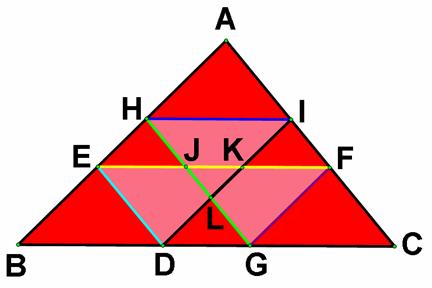
Looking at the intersection points J, K, and L in some directions of his walk, we will see that , , and are congruent. Also, these triangles are congruent to , , and . Besides, , , and are congruent.

Let’s explore this conjecture in the GSP file by clicking HERE.

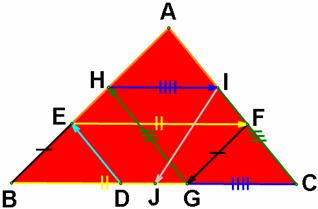
We will use the fact that the two triangles divided by the diagonal of the parallelogram are congruent.

Consider in the parallelogram BEKD, we have .

In the parallelogram GJFC, . Also, in the parallelogram AHLI.

Since BD = HI = GC, DE = CF = IA, and EB = FG = AH, by the SSS congruence , , and are congruent. Therefore, , , , , , and are congruent.

By the fact of the parallelogram, AE = HB = ID, EF = BG = DC, and FA = GH = CI. So, , , and are congruent by SSS congruence.

With the properties of parallelogram, we can also have other conjectures as the following.

If the starting point of Barney lies outside the segment BC, we also get the results the same as it lies on the segment BC. In other words, Barney will finally return to the starting point after reaching the wall for 5 times.

If Barney walks from the point D on a line BC outside the segment BC, we have

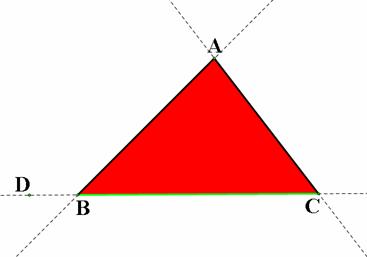
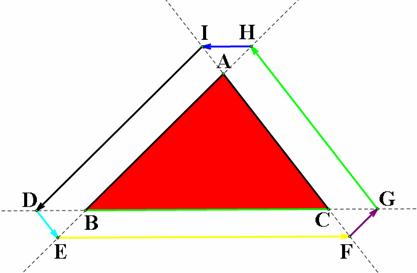
We have the conjecture that and for D is on the left of B outside the segment BC.

Similarly by changing the alphabetical order, we have the conjecture in the case of D on the right of B outside BC. The figures below can give us the ideas in proving the conjecture.

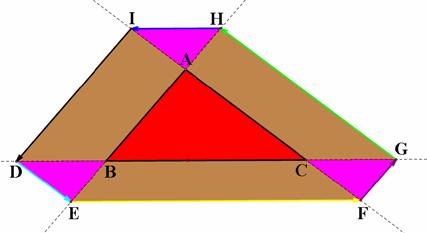
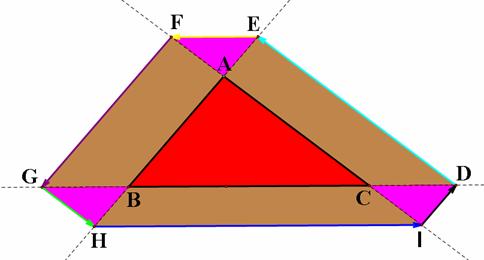
Click HERE to investigate this conjecture in GSP file.

The proofs of these cases still need the properties of parallelogram and the axiom of congruence.

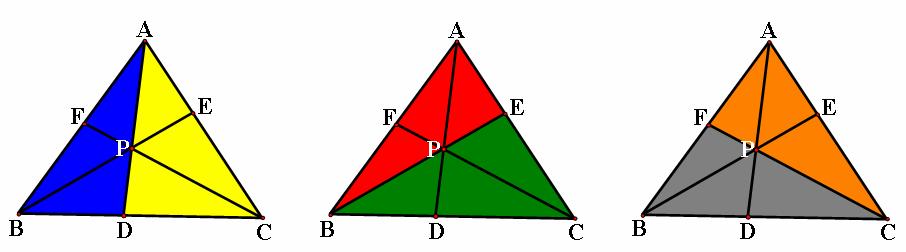
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F, respectively.

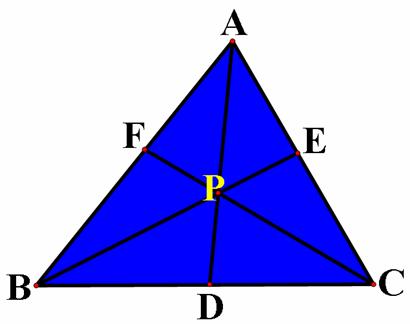
Click HERE to explore the relationship of the segments of perimeter.

We define a cevian as the line segment joining a vertex of a triangle to any given point on the opposite side.

If AD, BE, and CF called the cevians are concurrent, then

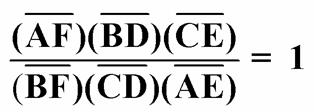
Conversely, if this equation holds for points D, E, and F on the three sides BC, AC, and AB respectively, the three sides AD, BE, and CF are concurrent.

From the concurrency of AD, BE, and CF, we can employ the fact of the areas of the triangles with the equal altitudes are the proportional of the bases of the triangles.

Let .

So, we have

.

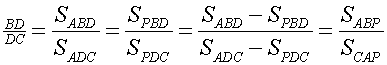Likewise,

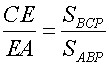, and .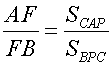

We therefore obtain

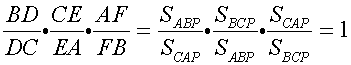
Conversely, assume the product of 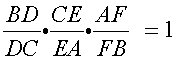is resulted from the cevians AD, BE, and CF such that D, E, and F are on the opposite sides of the vertices A, B, and C, respectively.

We will show that these three cevians are concurrent.

Suppose the cevians AD and BE meet at P.

The third cevian through this point P is CG. By the previous proof we have

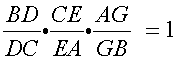but we have assume that .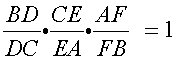

So, = . This suggests that G and F are the same points.

Hence, AD, BE, and CF are concurrent.

As the cevian is the line segment joining a vertex of a triangle to any given point on the opposite side, it is convenient to apply the Ceva’s Theorem for proving the concurrency.

We will see that this theorem is useful to prove of the concurrency of the medians (if P is the centroid), the lines of the altitudes (if P is the orthocenter), and the bisectors of the angles (if P is the incenter) or other special point P.

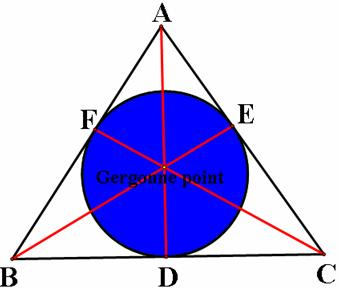
For example, Gergonne point which is defined by giving D, E, F be the points where the inscribed circle touches the sides of the triangle ABC. Then the lines AD, BE and CF intersect at one point.

Click HERE to investigate some relationship in the GSP file.

These can still use the Ceva’s theorem in the proof because they are type of the cevians. Besides showing the concurrency of segments, we also have AF = EA, FB = BD, DC = CE.

Also, the Ceva’s Theorem is used in showing the symmedians meet at a point called Lemoine point, in proving the concurrency of three lines are concurrent at the Nagel point. If let be the point of tangency of side BC and the excircle with center . Similarly define points and on sides AC and AB.

Also, the Ceva’s Theorem still covers in case that P lies outside the triangle. This may represent the advantage of this theorem that gives us an interesting relation of what we call “the cevians.”

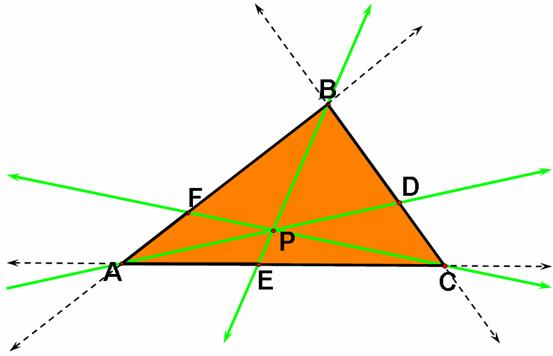
Click HERE to explore a generalization of the result that the point P can be outside the triangle.

RETURN