Complex Numbers and Angle Addition Formulas

By: Kelli Parker

As a math student, I have struggled with remembering the angle addition formulas for sine and cosine. The two formulas are so similar, it can be very easy to mix them up, but it would be deadly to do so on an exam. A recent assignment for a math education class helped me realize that I can use multiplication of complex numbers to help remember these two formulas!

First, recall the sine and cosine angle addition formulas:

Certainly, there are beautiful trigonometric proofs we could do, using identities and substitution. Instead of using trig, however, we can follow the pattern of integrated mathematics and use a completely different topic, complex numbers, to explain and remember these formulas.

Now for a little review of complex number “anatomy”:

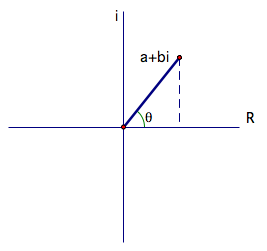
Take a complex number, z = a + bi. We can think of z like a vector, with “x and y” components, which are in this case, “real and imaginary”. We call a the “real” component because it has no i term in it. Looking at the plot of z above in the Real-Complex plane, the a term is the component on the horizontal, or real, axis. Our b is like a scalar which we multiply to i. We call bi the imaginary component of our complex number because of the i term; we see the imaginary component on the vertical, or “i” axis in our plot above.

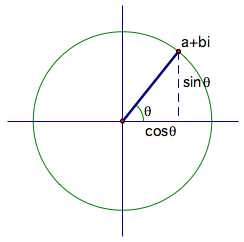
We can also represent z in polar form. We do this by first finding the angle between the real axis and z, which we call . Allow z to be a radius of a unit circle. The coordinates for the endpoint of z that lies on the unit circle can be obtained as on the normal trig unit circle: by bringing in sine and cosine. Recall that this is done by creating a right triangle with hypotenuse z, as in the plot below. So we can now use our trig relationships and see that the sides of this triangle make up the components of z. Where before we had a for the real part, we now can use cos; similarly for the imaginary part, instead of using b, we can use sin. Since it is a rare occasion that z would have a length (or modulus) of 1, we will call its length r. Since our cosine and sine relationships were based on a hypotenuse of 1, we can just multiply by r to get the correct value.

So now our complex number is represented in polar form:

Now that we’ve looked at the polar form of z, let’s choose two more complex numbers, x and y. We will represent them in the first way: x = c+di and y = m+ni. Let’s look at the product of x and y:

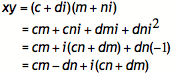
Notice that we combine the real components in the first 2 terms (those terms not containing i) and the imaginary components in the last 2. We are able to substitute -1 for i² because this is a property of i.

Next, let’s consider x and y in their polar form. For ease of notation, we will call the angle for x angle(x), and we will call the angle for y angle(y), noting and understanding that these are not equivalent with the numbers themselves. We will also take an r value of 1, for simpler calculation. So we have x = cos(x)+ isin(x), and

y = cos(y)+ isin(y). Let’s look at the product in polar form:

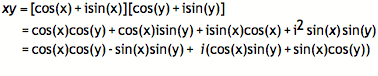
We have something that looks like a combination of the two angle addition formulas, but is still the product of 2 complex numbers. It corresponds exactly to the general form product we took above; the corresponding values of the two forms would be c = cos(x), d = sin(x), m = cos(y), and n = sin(y). So if we substitute the cosine and sine values into the general form product we found above, we obtain the following:

So when we combine the real components, we get cos(x)cos(y) – sin(x)sin(y). Remember that in polar form, the cosine value corresponds to the real component. So for the cosine part of the complex number, we have obtained the cosine angle addition formula! The same is true if we look at the imaginary part, the coefficient of i:

cos(x)sin(y)+ sin(x)cos(y), which is the sine angle addition formula, since sine corresponds to the coefficient of the imaginary part of complex numbers!

Next time memory fails and you can’t remember which formula is which, think about multiplying 2 complex numbers, and then substitute the sine and cosine values of the polar form into the product, and after you group reals and imaginaries together, you’ll have your angle addition formulas.

Go back to Kelli’s page